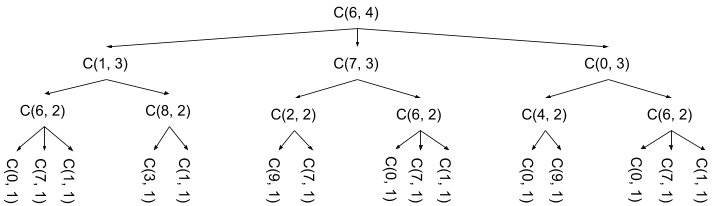
As an engineer and interviewer at Google, today is the second time I have posted to share interview suggestions for technology companies. Here is a statement: This article only represents my personal observations, opinions and suggestions. Do not treat it as an official recommendation or statement from Google or Alphabet. The following question is the first question in my interview career; it is also the first to be leaked and the first to be banned. I like this question because it has the following advantages: The problem is easy to articulate and easy to understand. There are multiple solutions to this problem. Each solution requires varying degrees of algorithm and data structure knowledge. Moreover, a little bit of foresight is needed. Each solution can be implemented in a few simple lines of code, which is very suitable for time-limited interviews. If you are a student or a job seeker, I hope you can understand through this article how interview questions generally look like. If you are also an interviewer, I am happy to share my style and ideas in the interview, how to better convey information and solicit opinions. Note that I will use Python to write code; I like Python because it is easy to learn, concise, and has a large standard library. Many interviewers I met also liked it very much. Although we implemented the "no language restriction" policy, 90% of the people I interviewed use Python. Also, I use Python 3 because, please, this is 2018. Think of your phone’s dial-up page as a chessboard. The chess piece can only move in the shape of "L", with two moves horizontally and one step vertically; or two moves vertically and one step horizontally. Now, suppose you can only dial the "L" shape like a chess piece. Dial the number once every time you finish an "L" shape, the starting position is also counted as one dial. Question: Starting from a certain point, within N steps, how many different numbers can you dial? discuss Every interview, I basically divide it into two parts: first we find out the algorithm scheme, and then let the interviewer implement it in the code. I said "we find an algorithm solution" because I am not a silent dictator in this process. Under such high pressure, 45 minutes is not enough to design and implement an algorithm. I usually let interviewees lead the discussion and let them generate ideas. Well, I am right by the side and leak a little bit of "chance" from time to time. The more capable the interviewers, the fewer "chances" I need to leak; but so far, I haven't met an interviewer who doesn't need my prompts at all. I want to emphasize one point. The most important thing is: As an interviewer, my job is not to sit around and watch everyone fail. I want to give you positive feedback and give you the opportunity to show what everyone is best at. To give them a hint is like saying: Now, I will pave you this step, but this is just to show me that you can go further on the road behind. After listening to the interviewer’s questions, what should you do? Remember not to write the code right away, but try to decompose the problem step by step on the blackboard. Breaking down the problem can help you find patterns, special cases, etc., and gradually form solutions in your brain. For example, if you start with the number 6 and can take 2 steps, there will be the following combinations: 6–1–8 6–1–6 6–7–2 6–7–6 6–0–4 6–0–6 There are 6 combinations in total. You can try to draw on paper with a pencil. Believe me, sometimes unexpected things happen when you try to solve the problem, which is more magical than staring in your head. How about it? Do you have a plan in mind? Tier 0: To the next step Using this question to interview, what surprises me most is that too many people are stuck in calculating how many possibilities are there when jumping out from a certain point, that is, neighbors. My suggestion is: when you are not sure, write a placeholder first, and then ask the interviewer whether to implement this part later. The complexity of this question is not in the calculation of Neighbors; what I care about is how you calculate the total. All the time spent calculating Neighbors is actually wasted. I will accept "Let's suppose there is a function that gives me Neighbors". Of course, I may also let you have time to implement this step later, you just need to write like this, and then continue. Moreover, if the complexity of a question is not here, you can also ask me if I can skip it first, generally I allow it. I don't mind that the interviewer doesn't know the complexity of the question, especially when they don't fully understand the problem at first. As for the Neighbors function, because the number never changes, you can write a Map directly and return the corresponding value. Level 1: Recursion Smart, you may have noticed that this problem can be calculated by enumerating all eligible numbers. Here you can use recursion to generate these values: This method can and is the most common method in interviews. But please note that we have generated so many numbers but haven't used them. After we have counted them, we never touch them again. So I suggest that everyone encounters this situation, try to think about whether there is a better solution. Level 2: Countless How to calculate the number without generating these numbers? It can be done, but it requires a little wit. Note that the number of digits that can be dialed N times from a specific point is equal to the sum of the digits that can be dialed N-1 times from all adjacent points. We can express it as this recursive relationship: If you think about it this way, it will be very intuitive. When you jump once: 6 has 3 neighbors (1, 7 and 0). When you jump 0 times, each number counts once, so you can only dial 3 each time. number. How could such a witty idea arise? In fact, if you learn recursion and study it on the blackboard, this will become obvious. So you can continue to solve this problem. In fact, there are many ways to achieve this. The following is the most common in interviews: That's it, combine this function to calculate neighbors. At this time, you can squeeze your shoulders and rest, because by this point, you have already wiped out a lot of people. The next question I often ask: What is the theoretical speed of the algorithm of this scheme? In this implementation, each call to count_sequences() will recursively call count_sequences() at least 2 times, because each number has at least 2 neighbors. This will cause the runtime to grow exponentially. It's okay for the number of jumps from 1 to 20, but we will hit a wall when we get to a larger number. 500 times may require the heat of the entire universe to complete the calculation. Level 3: Memory So, can we do better? Use the above method, and can't. I like this question because it can bring out everyone's wisdom layer by layer and find more efficient methods. In order to find a better way, let us see how this function is called, take count_sequences(6, 4) as an example. Note that C is used as the function name to simplify. You may have noticed that C(6, 2) is run 3 times, each time it is the same operation and returns the same value. The most critical point here is these repeated calculations. Every time you use their values, there is no need to calculate them again. how to solve this problem? memory. We have the same function calls and results instead of letting them repeat. In this way, we can directly give the previous results later. The implementation method is as follows: Tier 4: Dynamic Design If you look at the previous recursive relationship again, you will find that the recursive memory scheme also has some limitations: Note that the result of skipping N times only depends on the result of the call after skipping N-1 times. At the same time, the cache contains all the results of each time. The reason I say this is a small limitation, because it does not cause real problems. When the number of jumps increases, the cache only increases linearly. But, after all, this is still not efficient enough. How to do? Let's take a look at the program and code again. Note that the code starts from the largest number of times, and then recurses directly to the smallest number: If you think of the entire function call graph as some kind of virtual tree, you will find that we are implementing a depth-first strategy. This is not a problem, but it does not make use of the attribute of shallow dependency. How to implement the breadth first strategy? Here is one way to achieve it: How is this version better than the previous recursive version? In fact, it is not much better, but this is not recursive, so it is difficult to crash even when dealing with very large data. Second, it uses constant memory; in the end, it still grows linearly, and it takes less than 20 seconds to process 200,000 jumps. Evaluate At this point, it's basically over. Designing and implementing a linear, output memory solution is a very good result in the interview. In my interview, if an interviewer writes a dynamic programming design, I usually give him a very high evaluation: excellent! When evaluating algorithms and data structures, I often say: The interviewer has a clear understanding of the problem and considers all possible aspects. When he points out the shortcomings, he can quickly improve and improve; finally, a good solution is achieved. . When evaluating code, my ideal statement is: the interviewer quickly and accurately converts ideas into code; the code structure is rigorous and easy to read. All special cases are summarized, and the code is carefully checked and tested to ensure that there are no bugs. Summarize I know, this interview question seems a bit scary, especially the whole explanation is very cumbersome. But the purpose of this article is completely different from the interview. Finally, some interview-related skills, as well as some good habits, share with you: Be sure to do it manually, starting from the smallest problem. When your program is doing useless calculations, you must pay attention to optimization. Reducing unnecessary calculations can make your solution more concise, and maybe you can find a more efficient solution. Know your recursive function. In actual production, recursion is often prone to problems, but it is still a very powerful algorithm design and strategy. Recursive schemes always have room for optimization and improvement. Always look for opportunities for memory. If your function is purposeful and will call the same value multiple times, then try to store it. MC4 connectors are a type of electrical connector used in photovoltaic (PV) solar power systems. They are designed to connect solar panels together and to the inverters or charge controllers that convert the DC power produced by the panels into AC power that can be used in homes and businesses. Waterproof Solar Panel Connectors,Diodes Solar Connector Mc4,Hot Sale Solar PV Cable Connector,PV Panel Wire MC4 Connector Ruitian Cable CO.,LTD. , https://www.rtlinecable.com

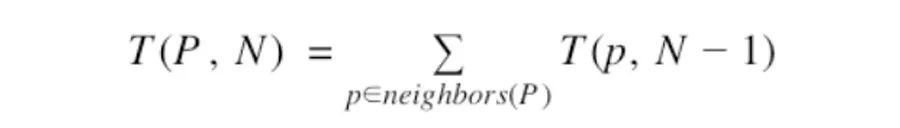


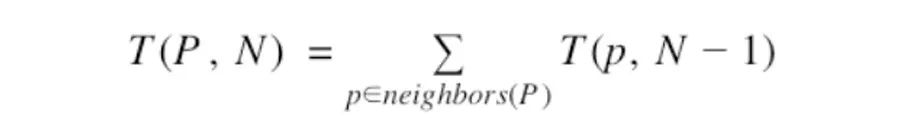


The MC4 connector is a simple and reliable connector that is easy to install and use. It has a locking mechanism that ensures a secure connection and prevents accidental disconnection. The connector is also weather-resistant and can withstand exposure to harsh outdoor conditions.
MC4 connectors come in two types: male and female. The male connector has a metal pin that fits into the female connector's socket, and the female connector has a metal socket that receives the male connector's pin. The connectors are color-coded to prevent confusion during installation, with red indicating the positive (+) connection and black indicating the negative (-) connection.
Overall, MC4 connectors are an essential component of any solar power system, providing a safe and reliable way to connect solar panels and other components.