Hi! I am very glad to see you coming in to read this article. Please don't mind, the title is a bit long and awkward (completely for seo considerations), but it is also a summary of the content of this article. If you are going to develop the scene shown below, but you have no good ideas, then this article will definitely help you! In fact, this kind of problem is actually a mathematical geometry application. Since it is a math problem, the first step in the routine of the examination is definitely a set of formulas. In this scenario, there are not many core formulas, just two: There is nothing to say in the first one. The second grade mathematics begins to teach the knowledge of a function, which is used to calculate the intersection of the route and the boundary of the plot. The second is a very classic compound transformation matrix, which is the displacement matrix fork-multiplied rotation matrix fork-multiplied displacement scaling matrix. We set the cross-multiplication result to A, then we can list the following equations: The calculation process is. . . Crossing vertical and horizontal multiplication vertical and horizontal multiplication vertical and horizontal multiplication vertical and horizontal multiplication vertical and horizontal multiplication vertical and horizontal multiplication vertical and horizontal multiplication vertical. . . . The algebra that is finally used for the program is: See here, congratulations, you have completed 50% of the workload! If you are in the exam, you will list the two formulas, and you will have half the score without writing the answer. A rectangular plot with the route level on the x-axis: Then, the latitude and longitude of the four vertices of the rectangle are now known, and the interval of flight of the drone is also known. It is unknown how many latitude lines the rectangle needs to intersect, and the
As a mobile multi-purpose platform, tablet computers also provide many possibilities for mobile teaching. The touch-based learning & entertainment teaching platform allows children to efficiently improve their academic performance in a relaxed and pleasant atmosphere. Such tablet computers generally integrate two learning sections of various courses and systematic learning functions. Generally, it includes multi-disciplinary high-quality teaching resources. The education tablet has the following main functions: it has the functions of touch screen input, text editing, picture editing, data storage, data management, wired and wireless Internet access that ordinary tablet computers have; Management functions, search methods support manual search, query by keyword, query by time; text and pictures can be scanned and converted into documents to save.
Education Tablet,learning tablet,leaning machine,New learning tablet Jingjiang Gisen Technology Co.,Ltd , https://www.jsgisengroup.com Written in front
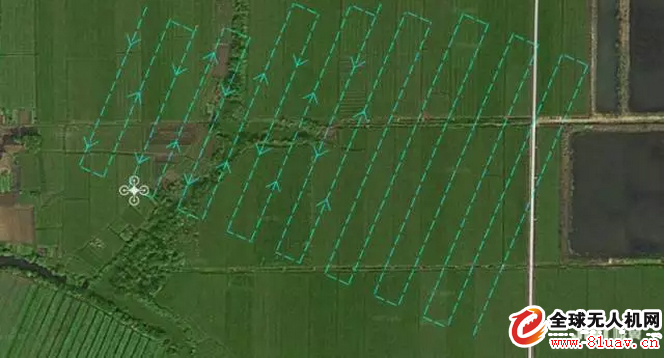
Reciprocating sport route

Reciprocating route planning based on irregular convex polygon plots
Oh, yes, the implementation of this article is based on a web platform map, using javascript. If you are also developing on a web platform, and the task time is very urgent, there is no time to read the full text. . . I have packaged the idea of ​​this article into a library, you can smash the link below, out of the box:
github.com/Char-Ten/cp...
Compatible with all major map platform apis (in fact, the impact of different platform api differences is very low) Oh, unbelieving words stamp demo:
Baidu map demo
Gao De map demo
Leaflet map demo
If you feel good, remember to give a star ~ original is not easy, thank you for your support text!
In fact, it is also a formula
![]()
One-time function two-point expression 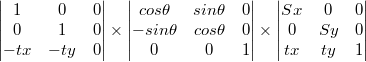
Scale the transformation matrix of SxSy times after rotating n degrees around the (tx, ty) point 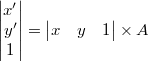
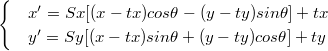
Through this formula, the coordinate point after the rotation of the route can be calculated.
Then we package them separately and make a function call first:

Start with the simplest scenario
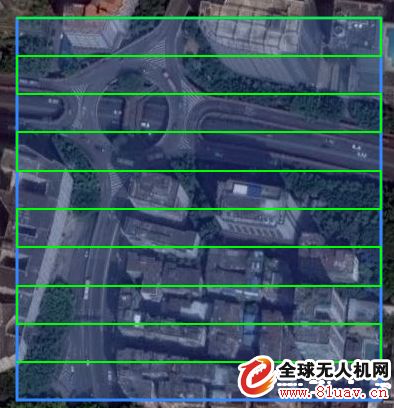
This is probably a size of 200 x 200 rectangle, the apex latitude and longitude of the upper left corner nw (northwest), the apex latitude and longitude of the upper right corner for the ne (Northeast), the apex latitude and longitude for the lower right corner of se (southeast), the apex latitude and longitude of the lower left corner For sw (southwest), set the drone flight interval to 10. You don't consider the connection order of the polylines first, just consider how each horizontal line is generated. Observe that you will find the following rules: y=N , and N is a constant, indicating a certain latitude value. y=N and the rectangle, that is, each horizontal line segment is the result of the intersection of the rectangular land and the dimension. N of each horizontal line is unknown. The latitude of two points to the left and right of a horizontal line segment is unknown. According to the known unknown, your goal has been very clear, a very simple geometric problem:
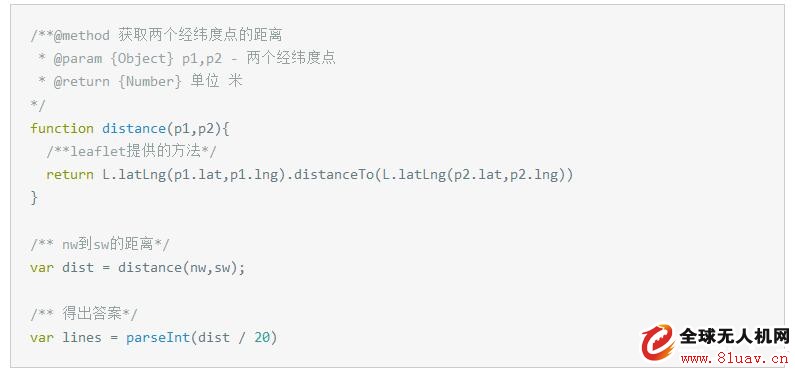
N for each horizontal line:

å› ä¸ºçŸ©å½¢çš„ä¸¤æ¡è¾¹æ˜¯åž‚直的,所以,横线段左å³ä¸¤ä¸ªç‚¹çš„ç»åº¦åˆ†åˆ«ä¸º nw.lng , ne.lng ã€‚è¿™æ ·æˆ‘ä»¬å°±å¯ä»¥ç»˜åˆ¶å‡ºæ¥äº†ï¼š 
èªæ˜Žçš„ä½ ä¸€å®šå‘现了,平行四边形在Yè½´ä¸Šçš„æŠ•å½±æ ¹æœ¬æ²¡æœ‰å‘生å˜åŒ–嘛,å³ä½¿å˜äº†ä¹‹åŽï¼Œç©¿è¿‡åœ°å—的纬度线数目还是ä¸å˜å˜›ï¼Œåªä¸è¿‡ï¼Œè¿™æ¬¡å› 为两æ¡è¾¹ä¸æ˜¯åž‚直的,所以,我们需è¦è®¡ç®—斜边与纬度线的交点。ç‰ç‰ï¼Œä½ 这时候想起了,最开始50%工作é‡é‡Œé¢æ‰€å°è£…的那个calcPointInLineWithY函数ï¼
ä½ å·²ç»çŸ¥é“斜边两个点的åæ ‡ï¼Œç„¶åŽä½ åˆçŸ¥é“y=N ï¼Œé‚£ä½ é€šè¿‡ä¸€æ¬¡å‡½æ•°çš„ä¸¤ç‚¹è¡¨è¾¾å¼ï¼Œå®Œå…¨å°±å¯ä»¥çŸ¥é“x ,也就是ç»åº¦æ˜¯å¤šå°‘å•¦ï¼šé‚£ä½ å¯ä»¥å†å˜ä¸€å˜ï¼Œè®©y轴上的投影也å‘生å˜åŒ–,就åƒè¿™æ ·ï¼š 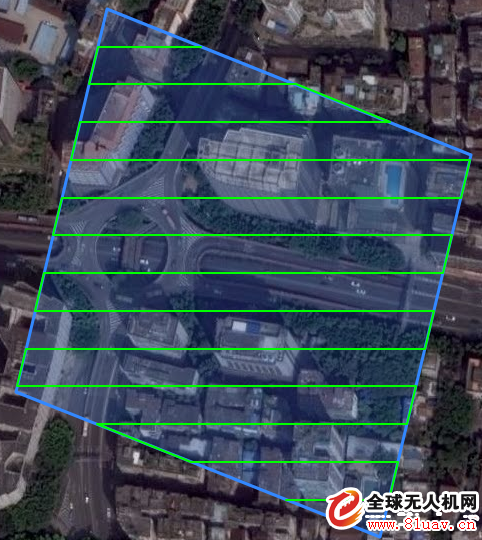
å¥½äº†ï¼Œè¿™ä¸‹ä½ è§‚å¯Ÿåˆ°ï¼Œæ¯æ¡è¾¹éƒ½è·Ÿçº¬åº¦çº¿ç›¸äº¤äº†ï¼Œä¹Ÿå°±æ˜¯è¯´ï¼Œè¿™æ¬¡ä½ è¦é历一下这个平行四边形四个顶点。ç‰ç‰ï¼Œä½ 似乎忘记了一个问题,这个四边形在y轴上的投影å‘生了å˜åŒ–,相交纬度线数目也跟ç€å‘生å˜åŒ–äº†ã€‚è¿™æ—¶å€™ä½ æƒ³åˆ°ï¼Œè¦ä¸ç»™è¿™ä¸ªå¤šè¾¹å½¢åšä¸ªå¤–接矩形?就åƒè¿™æ ·ï¼š 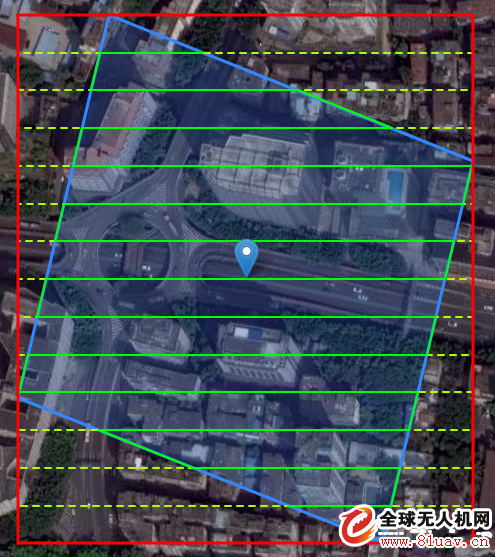
è¿™æ ·æ˜¯ä¸æ˜¯åˆå›žå½’了最开始的场景?åªæ˜¯æŠŠcalcPointInLineWithYå‡½æ•°åŠ ä¸ŠåŽ»ä¹‹åŽï¼Œä½ å¯ä»¥å¾—到任æ„凸多边形与纬度线相交的模型。
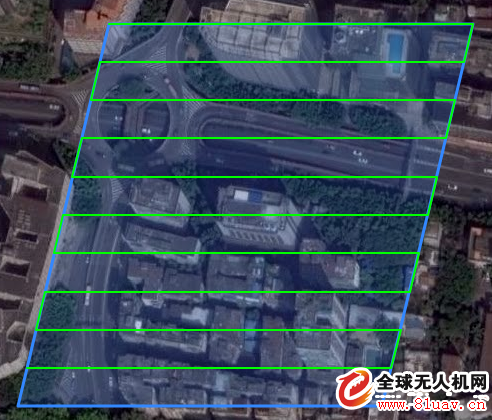
å› ä¸ºçŸ©å½¢çš„ä¸¤æ¡è¾¹æ˜¯åž‚直的,所以,横线段左å³ä¸¤ä¸ªç‚¹çš„ç»åº¦åˆ†åˆ«ä¸ºnw.lng , ne.lng ã€‚è¿™æ ·æˆ‘ä»¬å°±å¯ä»¥ç»˜åˆ¶å‡ºæ¥äº†ï¼š  场景开始å˜å½¢ï¼é”µé”µï¼Œæˆ‘们把矩形上é¢çš„边往东挪50米,得到一个平行四边形:
场景开始å˜å½¢ï¼é”µé”µï¼Œæˆ‘们把矩形上é¢çš„边往东挪50米,得到一个平行四边形: 
èªæ˜Žçš„ä½ ä¸€å®šå‘现了,平行四边形在Yè½´ä¸Šçš„æŠ•å½±æ ¹æœ¬æ²¡æœ‰å‘生å˜åŒ–嘛,å³ä½¿å˜äº†ä¹‹åŽï¼Œç©¿è¿‡åœ°å—的纬度线数目还是ä¸å˜å˜›ï¼Œåªä¸è¿‡ï¼Œè¿™æ¬¡å› 为两æ¡è¾¹ä¸æ˜¯åž‚直的,所以,我们需è¦è®¡ç®—斜边与纬度线的交点。ç‰ç‰ï¼Œä½ 这时候想起了,最开始50%工作é‡é‡Œé¢æ‰€å°è£…的那个calcPointInLineWithY函数ï¼
ä½ å·²ç»çŸ¥é“斜边两个点的åæ ‡ï¼Œç„¶åŽä½ åˆçŸ¥é“y=N ï¼Œé‚£ä½ é€šè¿‡ä¸€æ¬¡å‡½æ•°çš„ä¸¤ç‚¹è¡¨è¾¾å¼ï¼Œå®Œå…¨å°±å¯ä»¥çŸ¥é“x ,也就是ç»åº¦æ˜¯å¤šå°‘å•¦ï¼šé‚£ä½ å¯ä»¥å†å˜ä¸€å˜ï¼Œè®©y轴上的投影也å‘生å˜åŒ–,就åƒè¿™æ ·ï¼š 
å¥½äº†ï¼Œè¿™ä¸‹ä½ è§‚å¯Ÿåˆ°ï¼Œæ¯æ¡è¾¹éƒ½è·Ÿçº¬åº¦çº¿ç›¸äº¤äº†ï¼Œä¹Ÿå°±æ˜¯è¯´ï¼Œè¿™æ¬¡ä½ è¦é历一下这个平行四边形四个顶点。ç‰ç‰ï¼Œä½ 似乎忘记了一个问题,这个四边形在y轴上的投影å‘生了å˜åŒ–,相交纬度线数目也跟ç€å‘生å˜åŒ–äº†ã€‚è¿™æ—¶å€™ä½ æƒ³åˆ°ï¼Œè¦ä¸ç»™è¿™ä¸ªå¤šè¾¹å½¢åšä¸ªå¤–接矩形?就åƒè¿™æ ·ï¼š 
è¿™æ ·æ˜¯ä¸æ˜¯åˆå›žå½’了最开始的场景?åªæ˜¯æŠŠcalcPointInLineWithYå‡½æ•°åŠ ä¸ŠåŽ»ä¹‹åŽï¼Œä½ å¯ä»¥å¾—到任æ„凸多边形与纬度线相交的模型。
å› ä¸ºçŸ©å½¢çš„ä¸¤æ¡è¾¹æ˜¯åž‚直的,所以,横线段左å³ä¸¤ä¸ªç‚¹çš„ç»åº¦åˆ†åˆ«ä¸º nw.lng , ne.lng ã€‚è¿™æ ·æˆ‘ä»¬å°±å¯ä»¥ç»˜åˆ¶å‡ºæ¥äº†ï¼š 

èªæ˜Žçš„ä½ ä¸€å®šå‘现了,平行四边形在Yè½´ä¸Šçš„æŠ•å½±æ ¹æœ¬æ²¡æœ‰å‘生å˜åŒ–嘛,å³ä½¿å˜äº†ä¹‹åŽï¼Œç©¿è¿‡åœ°å—的纬度线数目还是ä¸å˜å˜›ï¼Œåªä¸è¿‡ï¼Œè¿™æ¬¡å› 为两æ¡è¾¹ä¸æ˜¯åž‚直的,所以,我们需è¦è®¡ç®—斜边与纬度线的交点。ç‰ç‰ï¼Œä½ 这时候想起了,最开始50%工作é‡é‡Œé¢æ‰€å°è£…的那个calcPointInLineWithY函数ï¼
ä½ å·²ç»çŸ¥é“斜边两个点的åæ ‡ï¼Œç„¶åŽä½ åˆçŸ¥é“y=N ï¼Œé‚£ä½ é€šè¿‡ä¸€æ¬¡å‡½æ•°çš„ä¸¤ç‚¹è¡¨è¾¾å¼ï¼Œå®Œå…¨å°±å¯ä»¥çŸ¥é“x ,也就是ç»åº¦æ˜¯å¤šå°‘å•¦ï¼šé‚£ä½ å¯ä»¥å†å˜ä¸€å˜ï¼Œè®©y轴上的投影也å‘生å˜åŒ–,就åƒè¿™æ ·ï¼š 
å¥½äº†ï¼Œè¿™ä¸‹ä½ è§‚å¯Ÿåˆ°ï¼Œæ¯æ¡è¾¹éƒ½è·Ÿçº¬åº¦çº¿ç›¸äº¤äº†ï¼Œä¹Ÿå°±æ˜¯è¯´ï¼Œè¿™æ¬¡ä½ è¦é历一下这个平行四边形四个顶点。ç‰ç‰ï¼Œä½ 似乎忘记了一个问题,这个四边形在y轴上的投影å‘生了å˜åŒ–,相交纬度线数目也跟ç€å‘生å˜åŒ–äº†ã€‚è¿™æ—¶å€™ä½ æƒ³åˆ°ï¼Œè¦ä¸ç»™è¿™ä¸ªå¤šè¾¹å½¢åšä¸ªå¤–接矩形?就åƒè¿™æ ·ï¼š 
è¿™æ ·æ˜¯ä¸æ˜¯åˆå›žå½’了最开始的场景?åªæ˜¯æŠŠcalcPointInLineWithYå‡½æ•°åŠ ä¸ŠåŽ»ä¹‹åŽï¼Œä½ å¯ä»¥å¾—到任æ„å‡¸å¤šè¾¹å½¢ä¸Žçº¬åº¦çº¿ç›¸äº¤çš„æ¨¡åž‹ã€‚å› ä¸ºçŸ©å½¢çš„ä¸¤æ¡è¾¹æ˜¯åž‚直的,所以,横线段左å³ä¸¤ä¸ªç‚¹çš„ç»åº¦åˆ†åˆ«ä¸º nw.lng , ne.lng ã€‚è¿™æ ·æˆ‘ä»¬å°±å¯ä»¥ç»˜åˆ¶å‡ºæ¥äº†ï¼š 

èªæ˜Žçš„ä½ ä¸€å®šå‘现了,平行四边形在Yè½´ä¸Šçš„æŠ•å½±æ ¹æœ¬æ²¡æœ‰å‘生å˜åŒ–嘛,å³ä½¿å˜äº†ä¹‹åŽï¼Œç©¿è¿‡åœ°å—的纬度线数目还是ä¸å˜å˜›ï¼Œåªä¸è¿‡ï¼Œè¿™æ¬¡å› 为两æ¡è¾¹ä¸æ˜¯åž‚直的,所以,我们需è¦è®¡ç®—斜边与纬度线的交点。ç‰ç‰ï¼Œä½ 这时候想起了,最开始50%工作é‡é‡Œé¢æ‰€å°è£…的那个calcPointInLineWithY函数ï¼
ä½ å·²ç»çŸ¥é“斜边两个点的åæ ‡ï¼Œç„¶åŽä½ åˆçŸ¥é“y=N ï¼Œé‚£ä½ é€šè¿‡ä¸€æ¬¡å‡½æ•°çš„ä¸¤ç‚¹è¡¨è¾¾å¼ï¼Œå®Œå…¨å°±å¯ä»¥çŸ¥é“x ,也就是ç»åº¦æ˜¯å¤šå°‘å•¦ï¼šé‚£ä½ å¯ä»¥å†å˜ä¸€å˜ï¼Œè®©y轴上的投影也å‘生å˜åŒ–,就åƒè¿™æ ·ï¼š 
å¥½äº†ï¼Œè¿™ä¸‹ä½ è§‚å¯Ÿåˆ°ï¼Œæ¯æ¡è¾¹éƒ½è·Ÿçº¬åº¦çº¿ç›¸äº¤äº†ï¼Œä¹Ÿå°±æ˜¯è¯´ï¼Œè¿™æ¬¡ä½ è¦é历一下这个平行四边形四个顶点。ç‰ç‰ï¼Œä½ 似乎忘记了一个问题,这个四边形在y轴上的投影å‘生了å˜åŒ–,相交纬度线数目也跟ç€å‘生å˜åŒ–äº†ã€‚è¿™æ—¶å€™ä½ æƒ³åˆ°ï¼Œè¦ä¸ç»™è¿™ä¸ªå¤šè¾¹å½¢åšä¸ªå¤–接矩形?就åƒè¿™æ ·ï¼š 
è¿™æ ·æ˜¯ä¸æ˜¯åˆå›žå½’了最开始的场景?åªæ˜¯æŠŠcalcPointInLineWithYå‡½æ•°åŠ ä¸ŠåŽ»ä¹‹åŽï¼Œä½ å¯ä»¥å¾—到任æ„å‡¸å¤šè¾¹å½¢ä¸Žçº¬åº¦çº¿ç›¸äº¤çš„æ¨¡åž‹ã€‚å› ä¸ºçŸ©å½¢çš„ä¸¤æ¡è¾¹æ˜¯åž‚直的,所以,横线段左å³ä¸¤ä¸ªç‚¹çš„ç»åº¦åˆ†åˆ«ä¸º nw.lng , ne.lng ã€‚è¿™æ ·æˆ‘ä»¬å°±å¯ä»¥ç»˜åˆ¶å‡ºæ¥äº†ï¼š 

èªæ˜Žçš„ä½ ä¸€å®šå‘现了,平行四边形在Yè½´ä¸Šçš„æŠ•å½±æ ¹æœ¬æ²¡æœ‰å‘生å˜åŒ–嘛,å³ä½¿å˜äº†ä¹‹åŽï¼Œç©¿è¿‡åœ°å—的纬度线数目还是ä¸å˜å˜›ï¼Œåªä¸è¿‡ï¼Œè¿™æ¬¡å› 为两æ¡è¾¹ä¸æ˜¯åž‚直的,所以,我们需è¦è®¡ç®—斜边与纬度线的交点。ç‰ç‰ï¼Œä½ 这时候想起了,最开始50%工作é‡é‡Œé¢æ‰€å°è£…的那个calcPointInLineWithY函数ï¼
ä½ å·²ç»çŸ¥é“斜边两个点的åæ ‡ï¼Œç„¶åŽä½ åˆçŸ¥é“y=N ï¼Œé‚£ä½ é€šè¿‡ä¸€æ¬¡å‡½æ•°çš„ä¸¤ç‚¹è¡¨è¾¾å¼ï¼Œå®Œå…¨å°±å¯ä»¥çŸ¥é“x ,也就是ç»åº¦æ˜¯å¤šå°‘å•¦ï¼šé‚£ä½ å¯ä»¥å†å˜ä¸€å˜ï¼Œè®©y轴上的投影也å‘生å˜åŒ–,就åƒè¿™æ ·ï¼š 
å¥½äº†ï¼Œè¿™ä¸‹ä½ è§‚å¯Ÿåˆ°ï¼Œæ¯æ¡è¾¹éƒ½è·Ÿçº¬åº¦çº¿ç›¸äº¤äº†ï¼Œä¹Ÿå°±æ˜¯è¯´ï¼Œè¿™æ¬¡ä½ è¦é历一下这个平行四边形四个顶点。ç‰ç‰ï¼Œä½ 似乎忘记了一个问题,这个四边形在y轴上的投影å‘生了å˜åŒ–,相交纬度线数目也跟ç€å‘生å˜åŒ–äº†ã€‚è¿™æ—¶å€™ä½ æƒ³åˆ°ï¼Œè¦ä¸ç»™è¿™ä¸ªå¤šè¾¹å½¢åšä¸ªå¤–接矩形?就åƒè¿™æ ·ï¼š 
è¿™æ ·æ˜¯ä¸æ˜¯åˆå›žå½’了最开始的场景?åªæ˜¯æŠŠcalcPointInLineWithYå‡½æ•°åŠ ä¸ŠåŽ»ä¹‹åŽï¼Œä½ å¯ä»¥å¾—到任æ„å‡¸å¤šè¾¹å½¢ä¸Žçº¬åº¦çº¿ç›¸äº¤çš„æ¨¡åž‹ã€‚å› ä¸ºçŸ©å½¢çš„ä¸¤æ¡è¾¹æ˜¯åž‚直的,所以,横线段左å³ä¸¤ä¸ªç‚¹çš„ç»åº¦åˆ†åˆ«ä¸º nw.lng , ne.lng ã€‚è¿™æ ·æˆ‘ä»¬å°±å¯ä»¥ç»˜åˆ¶å‡ºæ¥äº†ï¼š 

èªæ˜Žçš„ä½ ä¸€å®šå‘现了,平行四边形在Yè½´ä¸Šçš„æŠ•å½±æ ¹æœ¬æ²¡æœ‰å‘生å˜åŒ–嘛,å³ä½¿å˜äº†ä¹‹åŽï¼Œç©¿è¿‡åœ°å—的纬度线数目还是ä¸å˜å˜›ï¼Œåªä¸è¿‡ï¼Œè¿™æ¬¡å› 为两æ¡è¾¹ä¸æ˜¯åž‚直的,所以,我们需è¦è®¡ç®—斜边与纬度线的交点。ç‰ç‰ï¼Œä½ 这时候想起了,最开始50%工作é‡é‡Œé¢æ‰€å°è£…的那个calcPointInLineWithY函数ï¼
ä½ å·²ç»çŸ¥é“斜边两个点的åæ ‡ï¼Œç„¶åŽä½ åˆçŸ¥é“y=N ï¼Œé‚£ä½ é€šè¿‡ä¸€æ¬¡å‡½æ•°çš„ä¸¤ç‚¹è¡¨è¾¾å¼ï¼Œå®Œå…¨å°±å¯ä»¥çŸ¥é“x ,也就是ç»åº¦æ˜¯å¤šå°‘å•¦ï¼šé‚£ä½ å¯ä»¥å†å˜ä¸€å˜ï¼Œè®©y轴上的投影也å‘生å˜åŒ–,就åƒè¿™æ ·ï¼š 
å¥½äº†ï¼Œè¿™ä¸‹ä½ è§‚å¯Ÿåˆ°ï¼Œæ¯æ¡è¾¹éƒ½è·Ÿçº¬åº¦çº¿ç›¸äº¤äº†ï¼Œä¹Ÿå°±æ˜¯è¯´ï¼Œè¿™æ¬¡ä½ è¦é历一下这个平行四边形四个顶点。ç‰ç‰ï¼Œä½ 似乎忘记了一个问题,这个四边形在y轴上的投影å‘生了å˜åŒ–,相交纬度线数目也跟ç€å‘生å˜åŒ–äº†ã€‚è¿™æ—¶å€™ä½ æƒ³åˆ°ï¼Œè¦ä¸ç»™è¿™ä¸ªå¤šè¾¹å½¢åšä¸ªå¤–接矩形?就åƒè¿™æ ·ï¼š 
è¿™æ ·æ˜¯ä¸æ˜¯åˆå›žå½’了最开始的场景?åªæ˜¯æŠŠcalcPointInLineWithYå‡½æ•°åŠ ä¸ŠåŽ»ä¹‹åŽï¼Œä½ å¯ä»¥å¾—到任æ„凸多边形与纬度线相交的模型。
å› ä¸ºçŸ©å½¢çš„ä¸¤æ¡è¾¹æ˜¯åž‚直的,所以,横线段左å³ä¸¤ä¸ªç‚¹çš„ç»åº¦åˆ†åˆ«ä¸º nw.lng , ne.lng ã€‚è¿™æ ·æˆ‘ä»¬å°±å¯ä»¥ç»˜åˆ¶å‡ºæ¥äº†ï¼š 

èªæ˜Žçš„ä½ ä¸€å®šå‘现了,平行四边形在Yè½´ä¸Šçš„æŠ•å½±æ ¹æœ¬æ²¡æœ‰å‘生å˜åŒ–嘛,å³ä½¿å˜äº†ä¹‹åŽï¼Œç©¿è¿‡åœ°å—的纬度线数目还是ä¸å˜å˜›ï¼Œåªä¸è¿‡ï¼Œè¿™æ¬¡å› 为两æ¡è¾¹ä¸æ˜¯åž‚直的,所以,我们需è¦è®¡ç®—斜边与纬度线的交点。ç‰ç‰ï¼Œä½ 这时候想起了,最开始50%工作é‡é‡Œé¢æ‰€å°è£…的那个calcPointInLineWithY函数ï¼
ä½ å·²ç»çŸ¥é“斜边两个点的åæ ‡ï¼Œç„¶åŽä½ åˆçŸ¥é“y=N ï¼Œé‚£ä½ é€šè¿‡ä¸€æ¬¡å‡½æ•°çš„ä¸¤ç‚¹è¡¨è¾¾å¼ï¼Œå®Œå…¨å°±å¯ä»¥çŸ¥é“x ,也就是ç»åº¦æ˜¯å¤šå°‘å•¦ï¼šé‚£ä½ å¯ä»¥å†å˜ä¸€å˜ï¼Œè®©y轴上的投影也å‘生å˜åŒ–,就åƒè¿™æ ·ï¼š 
å¥½äº†ï¼Œè¿™ä¸‹ä½ è§‚å¯Ÿåˆ°ï¼Œæ¯æ¡è¾¹éƒ½è·Ÿçº¬åº¦çº¿ç›¸äº¤äº†ï¼Œä¹Ÿå°±æ˜¯è¯´ï¼Œè¿™æ¬¡ä½ è¦é历一下这个平行四边形四个顶点。ç‰ç‰ï¼Œä½ 似乎忘记了一个问题,这个四边形在y轴上的投影å‘生了å˜åŒ–,相交纬度线数目也跟ç€å‘生å˜åŒ–äº†ã€‚è¿™æ—¶å€™ä½ æƒ³åˆ°ï¼Œè¦ä¸ç»™è¿™ä¸ªå¤šè¾¹å½¢åšä¸ªå¤–接矩形?就åƒè¿™æ ·ï¼š 
è¿™æ ·æ˜¯ä¸æ˜¯åˆå›žå½’了最开始的场景?åªæ˜¯æŠŠcalcPointInLineWithYå‡½æ•°åŠ ä¸ŠåŽ»ä¹‹åŽï¼Œä½ å¯ä»¥å¾—到任æ„å‡¸å¤šè¾¹å½¢ä¸Žçº¬åº¦çº¿ç›¸äº¤çš„æ¨¡åž‹ã€‚å› ä¸ºçŸ©å½¢çš„ä¸¤æ¡è¾¹æ˜¯åž‚直的,所以,横线段左å³ä¸¤ä¸ªç‚¹çš„ç»åº¦åˆ†åˆ«ä¸º nw.lng , ne.lng ã€‚è¿™æ ·æˆ‘ä»¬å°±å¯ä»¥ç»˜åˆ¶å‡ºæ¥äº†ï¼š 

èªæ˜Žçš„ä½ ä¸€å®šå‘现了,平行四边形在Yè½´ä¸Šçš„æŠ•å½±æ ¹æœ¬æ²¡æœ‰å‘生å˜åŒ–嘛,å³ä½¿å˜äº†ä¹‹åŽï¼Œç©¿è¿‡åœ°å—的纬度线数目还是ä¸å˜å˜›ï¼Œåªä¸è¿‡ï¼Œè¿™æ¬¡å› 为两æ¡è¾¹ä¸æ˜¯åž‚直的,所以,我们需è¦è®¡ç®—斜边与纬度线的交点。ç‰ç‰ï¼Œä½ 这时候想起了,最开始50%工作é‡é‡Œé¢æ‰€å°è£…的那个calcPointInLineWithY函数ï¼
ä½ å·²ç»çŸ¥é“斜边两个点的åæ ‡ï¼Œç„¶åŽä½ åˆçŸ¥é“y=N ï¼Œé‚£ä½ é€šè¿‡ä¸€æ¬¡å‡½æ•°çš„ä¸¤ç‚¹è¡¨è¾¾å¼ï¼Œå®Œå…¨å°±å¯ä»¥çŸ¥é“x ,也就是ç»åº¦æ˜¯å¤šå°‘å•¦ï¼šé‚£ä½ å¯ä»¥å†å˜ä¸€å˜ï¼Œè®©y轴上的投影也å‘生å˜åŒ–,就åƒè¿™æ ·ï¼š 
å¥½äº†ï¼Œè¿™ä¸‹ä½ è§‚å¯Ÿåˆ°ï¼Œæ¯æ¡è¾¹éƒ½è·Ÿçº¬åº¦çº¿ç›¸äº¤äº†ï¼Œä¹Ÿå°±æ˜¯è¯´ï¼Œè¿™æ¬¡ä½ è¦é历一下这个平行四边形四个顶点。ç‰ç‰ï¼Œä½ 似乎忘记了一个问题,这个四边形在y轴上的投影å‘生了å˜åŒ–,相交纬度线数目也跟ç€å‘生å˜åŒ–äº†ã€‚è¿™æ—¶å€™ä½ æƒ³åˆ°ï¼Œè¦ä¸ç»™è¿™ä¸ªå¤šè¾¹å½¢åšä¸ªå¤–接矩形?就åƒè¿™æ ·ï¼š 
è¿™æ ·æ˜¯ä¸æ˜¯åˆå›žå½’了最开始的场景?åªæ˜¯æŠŠcalcPointInLineWithYå‡½æ•°åŠ ä¸ŠåŽ»ä¹‹åŽï¼Œä½ å¯ä»¥å¾—到任æ„å‡¸å¤šè¾¹å½¢ä¸Žçº¬åº¦çº¿ç›¸äº¤çš„æ¨¡åž‹ã€‚å› ä¸ºçŸ©å½¢çš„ä¸¤æ¡è¾¹æ˜¯åž‚直的,所以,横线段左å³ä¸¤ä¸ªç‚¹çš„ç»åº¦åˆ†åˆ«ä¸º nw.lng , ne.lng ã€‚è¿™æ ·æˆ‘ä»¬å°±å¯ä»¥ç»˜åˆ¶å‡ºæ¥äº†ï¼š 

èªæ˜Žçš„ä½ ä¸€å®šå‘现了,平行四边形在Yè½´ä¸Šçš„æŠ•å½±æ ¹æœ¬æ²¡æœ‰å‘生å˜åŒ–嘛,å³ä½¿å˜äº†ä¹‹åŽï¼Œç©¿è¿‡åœ°å—的纬度线数目还是ä¸å˜å˜›ï¼Œåªä¸è¿‡ï¼Œè¿™æ¬¡å› 为两æ¡è¾¹ä¸æ˜¯åž‚直的,所以,我们需è¦è®¡ç®—斜边与纬度线的交点。ç‰ç‰ï¼Œä½ 这时候想起了,最开始50%工作é‡é‡Œé¢æ‰€å°è£…的那个calcPointInLineWithY函数ï¼
ä½ å·²ç»çŸ¥é“斜边两个点的åæ ‡ï¼Œç„¶åŽä½ åˆçŸ¥é“y=N ï¼Œé‚£ä½ é€šè¿‡ä¸€æ¬¡å‡½æ•°çš„ä¸¤ç‚¹è¡¨è¾¾å¼ï¼Œå®Œå…¨å°±å¯ä»¥çŸ¥é“x ,也就是ç»åº¦æ˜¯å¤šå°‘å•¦ï¼šé‚£ä½ å¯ä»¥å†å˜ä¸€å˜ï¼Œè®©y轴上的投影也å‘生å˜åŒ–,就åƒè¿™æ ·ï¼š 
å¥½äº†ï¼Œè¿™ä¸‹ä½ è§‚å¯Ÿåˆ°ï¼Œæ¯æ¡è¾¹éƒ½è·Ÿçº¬åº¦çº¿ç›¸äº¤äº†ï¼Œä¹Ÿå°±æ˜¯è¯´ï¼Œè¿™æ¬¡ä½ è¦é历一下这个平行四边形四个顶点。ç‰ç‰ï¼Œä½ 似乎忘记了一个问题,这个四边形在y轴上的投影å‘生了å˜åŒ–,相交纬度线数目也跟ç€å‘生å˜åŒ–äº†ã€‚è¿™æ—¶å€™ä½ æƒ³åˆ°ï¼Œè¦ä¸ç»™è¿™ä¸ªå¤šè¾¹å½¢åšä¸ªå¤–接矩形?就åƒè¿™æ ·ï¼š 
è¿™æ ·æ˜¯ä¸æ˜¯åˆå›žå½’了最开始的场景?åªæ˜¯æŠŠcalcPointInLineWithYå‡½æ•°åŠ ä¸ŠåŽ»ä¹‹åŽï¼Œä½ å¯ä»¥å¾—到任æ„å‡¸å¤šè¾¹å½¢ä¸Žçº¬åº¦çº¿ç›¸äº¤çš„æ¨¡åž‹ã€‚å› ä¸ºçŸ©å½¢çš„ä¸¤æ¡è¾¹æ˜¯åž‚直的,所以,横线段左å³ä¸¤ä¸ªç‚¹çš„ç»åº¦åˆ†åˆ«ä¸º nw.lng , ne.lng ã€‚è¿™æ ·æˆ‘ä»¬å°±å¯ä»¥ç»˜åˆ¶å‡ºæ¥äº†ï¼š 

èªæ˜Žçš„ä½ ä¸€å®šå‘现了,平行四边形在Yè½´ä¸Šçš„æŠ•å½±æ ¹æœ¬æ²¡æœ‰å‘生å˜åŒ–嘛,å³ä½¿å˜äº†ä¹‹åŽï¼Œç©¿è¿‡åœ°å—的纬度线数目还是ä¸å˜å˜›ï¼Œåªä¸è¿‡ï¼Œè¿™æ¬¡å› 为两æ¡è¾¹ä¸æ˜¯åž‚直的,所以,我们需è¦è®¡ç®—斜边与纬度线的交点。ç‰ç‰ï¼Œä½ 这时候想起了,最开始50%工作é‡é‡Œé¢æ‰€å°è£…的那个calcPointInLineWithY函数ï¼
ä½ å·²ç»çŸ¥é“斜边两个点的åæ ‡ï¼Œç„¶åŽä½ åˆçŸ¥é“y=N ï¼Œé‚£ä½ é€šè¿‡ä¸€æ¬¡å‡½æ•°çš„ä¸¤ç‚¹è¡¨è¾¾å¼ï¼Œå®Œå…¨å°±å¯ä»¥çŸ¥é“x ,也就是ç»åº¦æ˜¯å¤šå°‘å•¦ï¼šé‚£ä½ å¯ä»¥å†å˜ä¸€å˜ï¼Œè®©y轴上的投影也å‘生å˜åŒ–,就åƒè¿™æ ·ï¼š 
å¥½äº†ï¼Œè¿™ä¸‹ä½ è§‚å¯Ÿåˆ°ï¼Œæ¯æ¡è¾¹éƒ½è·Ÿçº¬åº¦çº¿ç›¸äº¤äº†ï¼Œä¹Ÿå°±æ˜¯è¯´ï¼Œè¿™æ¬¡ä½ è¦é历一下这个平行四边形四个顶点。ç‰ç‰ï¼Œä½ 似乎忘记了一个问题,这个四边形在y轴上的投影å‘生了å˜åŒ–,相交纬度线数目也跟ç€å‘生å˜åŒ–äº†ã€‚è¿™æ—¶å€™ä½ æƒ³åˆ°ï¼Œè¦ä¸ç»™è¿™ä¸ªå¤šè¾¹å½¢åšä¸ªå¤–接矩形?就åƒè¿™æ ·ï¼š 
è¿™æ ·æ˜¯ä¸æ˜¯åˆå›žå½’了最开始的场景?åªæ˜¯æŠŠcalcPointInLineWithYå‡½æ•°åŠ ä¸ŠåŽ»ä¹‹åŽï¼Œä½ å¯ä»¥å¾—到任æ„å‡¸å¤šè¾¹å½¢ä¸Žçº¬åº¦çº¿ç›¸äº¤çš„æ¨¡åž‹ã€‚å› ä¸ºçŸ©å½¢çš„ä¸¤æ¡è¾¹æ˜¯åž‚直的,所以,横线段左å³ä¸¤ä¸ªç‚¹çš„ç»åº¦åˆ†åˆ«ä¸º nw.lng , ne.lng ã€‚è¿™æ ·æˆ‘ä»¬å°±å¯ä»¥ç»˜åˆ¶å‡ºæ¥äº†ï¼š 

èªæ˜Žçš„ä½ ä¸€å®šå‘现了,平行四边形在Yè½´ä¸Šçš„æŠ•å½±æ ¹æœ¬æ²¡æœ‰å‘生å˜åŒ–嘛,å³ä½¿å˜äº†ä¹‹åŽï¼Œç©¿è¿‡åœ°å—的纬度线数目还是ä¸å˜å˜›ï¼Œåªä¸è¿‡ï¼Œè¿™æ¬¡å› 为两æ¡è¾¹ä¸æ˜¯åž‚直的,所以,我们需è¦è®¡ç®—斜边与纬度线的交点。ç‰ç‰ï¼Œä½ 这时候想起了,最开始50%工作é‡é‡Œé¢æ‰€å°è£…的那个calcPointInLineWithY函数ï¼
ä½ å·²ç»çŸ¥é“斜边两个点的åæ ‡ï¼Œç„¶åŽä½ åˆçŸ¥é“y=N ï¼Œé‚£ä½ é€šè¿‡ä¸€æ¬¡å‡½æ•°çš„ä¸¤ç‚¹è¡¨è¾¾å¼ï¼Œå®Œå…¨å°±å¯ä»¥çŸ¥é“x ,也就是ç»åº¦æ˜¯å¤šå°‘å•¦ï¼šé‚£ä½ å¯ä»¥å†å˜ä¸€å˜ï¼Œè®©y轴上的投影也å‘生å˜åŒ–,就åƒè¿™æ ·ï¼š 
å¥½äº†ï¼Œè¿™ä¸‹ä½ è§‚å¯Ÿåˆ°ï¼Œæ¯æ¡è¾¹éƒ½è·Ÿçº¬åº¦çº¿ç›¸äº¤äº†ï¼Œä¹Ÿå°±æ˜¯è¯´ï¼Œè¿™æ¬¡ä½ è¦é历一下这个平行四边形四个顶点。ç‰ç‰ï¼Œä½ 似乎忘记了一个问题,这个四边形在y轴上的投影å‘生了å˜åŒ–,相交纬度线数目也跟ç€å‘生å˜åŒ–äº†ã€‚è¿™æ—¶å€™ä½ æƒ³åˆ°ï¼Œè¦ä¸ç»™è¿™ä¸ªå¤šè¾¹å½¢åšä¸ªå¤–接矩形?就åƒè¿™æ ·ï¼š 
è¿™æ ·æ˜¯ä¸æ˜¯åˆå›žå½’了最开始的场景?åªæ˜¯æŠŠcalcPointInLineWithYå‡½æ•°åŠ ä¸ŠåŽ»ä¹‹åŽï¼Œä½ å¯ä»¥å¾—到任æ„å‡¸å¤šè¾¹å½¢ä¸Žçº¬åº¦çº¿ç›¸äº¤çš„æ¨¡åž‹ã€‚å› ä¸ºçŸ©å½¢çš„ä¸¤æ¡è¾¹æ˜¯åž‚直的,所以,横线段左å³ä¸¤ä¸ªç‚¹çš„ç»åº¦åˆ†åˆ«ä¸º nw.lng , ne.lng ã€‚è¿™æ ·æˆ‘ä»¬å°±å¯ä»¥ç»˜åˆ¶å‡ºæ¥äº†ï¼š 

èªæ˜Žçš„ä½ ä¸€å®šå‘现了,平行四边形在Yè½´ä¸Šçš„æŠ•å½±æ ¹æœ¬æ²¡æœ‰å‘生å˜åŒ–嘛,å³ä½¿å˜äº†ä¹‹åŽï¼Œç©¿è¿‡åœ°å—的纬度线数目还是ä¸å˜å˜›ï¼Œåªä¸è¿‡ï¼Œè¿™æ¬¡å› 为两æ¡è¾¹ä¸æ˜¯åž‚直的,所以,我们需è¦è®¡ç®—斜边与纬度线的交点。ç‰ç‰ï¼Œä½ 这时候想起了,最开始50%工作é‡é‡Œé¢æ‰€å°è£…的那个calcPointInLineWithY函数ï¼
ä½ å·²ç»çŸ¥é“斜边两个点的åæ ‡ï¼Œç„¶åŽä½ åˆçŸ¥é“y=N ï¼Œé‚£ä½ é€šè¿‡ä¸€æ¬¡å‡½æ•°çš„ä¸¤ç‚¹è¡¨è¾¾å¼ï¼Œå®Œå…¨å°±å¯ä»¥çŸ¥é“x ,也就是ç»åº¦æ˜¯å¤šå°‘å•¦ï¼šé‚£ä½ å¯ä»¥å†å˜ä¸€å˜ï¼Œè®©y轴上的投影也å‘生å˜åŒ–,就åƒè¿™æ ·ï¼š 
å¥½äº†ï¼Œè¿™ä¸‹ä½ è§‚å¯Ÿåˆ°ï¼Œæ¯æ¡è¾¹éƒ½è·Ÿçº¬åº¦çº¿ç›¸äº¤äº†ï¼Œä¹Ÿå°±æ˜¯è¯´ï¼Œè¿™æ¬¡ä½ è¦é历一下这个平行四边形四个顶点。ç‰ç‰ï¼Œä½ 似乎忘记了一个问题,这个四边形在y轴上的投影å‘生了å˜åŒ–,相交纬度线数目也跟ç€å‘生å˜åŒ–äº†ã€‚è¿™æ—¶å€™ä½ æƒ³åˆ°ï¼Œè¦ä¸ç»™è¿™ä¸ªå¤šè¾¹å½¢åšä¸ªå¤–接矩形?就åƒè¿™æ ·ï¼š 
è¿™æ ·æ˜¯ä¸æ˜¯åˆå›žå½’了最开始的场景?åªæ˜¯æŠŠcalcPointInLineWithYå‡½æ•°åŠ ä¸ŠåŽ»ä¹‹åŽï¼Œä½ å¯ä»¥å¾—到任æ„凸多边形与纬度线相交的模型。