High-speed analog-to-digital converters (ADCs) have inherent limitations that occasionally cause rare conversion errors outside of their normal function. However, many actual sampling systems do not allow for high ADC conversion error rates. Therefore, it is important to quantify the frequency and amplitude of the high-speed analog-to-digital conversion error rate (CER).
The relatively sparse switching errors of high-speed or GSPS ADCs (gigasample ADCs per second) not only make them difficult to detect, but also make the measurement process time consuming. This duration typically exceeds the millisecond range, reaching hours, days, weeks, or even months. To help reduce this time-consuming test burden, the error rate can be estimated with certain "confidence" determinism while still maintaining the quality of the results.
Bit error rate (BER) and conversion error rate
Similar to the digital equivalent of BER in serial or parallel digital data transmission, CER is the ratio of the number of conversion errors to the total number of samples. However, there are some differences between BER and CER. The BER test in the digital data stream uses a long pseudo-random sequence that can be initiated in the transmitter using common seed values ​​at both ends of the transmission. The receiver is expected to receive the ideal transmission. By observing the difference between the received data and the ideal data, the BER can be accurately calculated. The mismatch in the pseudo-random sequence data between the two ends (based on the seed value) is considered as an error.
Unlike CERs, error determination is not as simple as a purely digital comparison. Due to the small nonlinearity of the ADC conversion process and the presence of system noise and jitter, it is not always possible to determine the exact difference between the expected data and the actual data. Instead, an error threshold needs to be established to determine the boundary between the conversion error and the sample with the expected noise. This is different from the digital BER and does not make an exact comparison of the expected data sent and received. Instead, the magnitude of the error in the sample must first be quantified and then determined to be a conversion error or within the expected nonlinear range of the converter and system. The bit error rate of the ADC's back-end digital interface must be lower than the converter's core CER, so it cannot be ignored. If this is not the case, the data output transmission error will cover the CER and become the main source of error.
Metastable
A common cause of conversion errors in high speed ADCs is a phenomenon known as metastable state. High-speed ADCs often use multiple step comparators at different stages in the conversion of analog signals to digital values. If the comparator cannot determine if the analog input is above or below its reference point, a metastable result can result in an error code. This can happen when the difference between the inputs of the two comparators is very small or zero, and a correct comparison cannot be made at this time. Because this error value propagates along the pipeline, the ADC can cause significant conversion errors.
When the differential analog input is a relatively large positive or negative value, the comparator can quickly calculate the difference and give a definitive decision. When the difference value is small or zero, the duration required for the comparator to make a decision can be much longer. If the comparator output latches before this decision point, a metastable result will result.
Some designs can alleviate this problem. First, the uncertainty range of the comparator is designed to be very small, forcing the comparator to make an accurate decision within the range of possible maximum analog input conditions. However, this can result in increased circuit power and design size.
The second method is to delay the comparator sampling time as much as possible, and establish the maximum time for the analog input to the known comparator output value. However, there are several limitations to this approach because the longest delay can only last until the end of the current sampling time, and the comparator must continue processing the next sample. The third method uses an intelligent error detection and correction algorithm that digitally compensates for the uncertainty introduced by the comparator during the subsequent stages of the high speed ADC conversion process. The logic can detect this miss when the comparator fails to make a decision within the maximum allowed time. This information can then be attached to the relevant sample for future internal adjustments. When this alert is recognized, a post-processing step can be used to correct the error before the sample is output from the converter. This can be seen in the AD9625 in Figure 1, which is a 12-bit, 2.5 GSPS ADC from Analog Devices.

Figure 1: Uncertainty of the comparator can be identified during the analog-to-digital conversion process of the AD9625. A correction command is executed in a subsequent step to correct the sample and then output from the converter.
Confidence
CER Confidence (CL) refers to the extrapolation of future errors in the event of inaccuracy to a specific failure rate. This reduces the total number of samples taken for a given CER, but at the cost of 100% certainty. From a mathematical point of view, to achieve absolute 100% certainty, you need to obtain samples for an infinite duration. Therefore, according to industry experience, the 95% confidence level is quite close to the known value, and the balance between uncertainty and measurement time is achieved. If the test is repeated a hundred times, there are 95 times to accurately identify the bit error rate. Sometimes engineers mistakenly believe that once an error is detected during the test, the process ends and the final CER is found. This is neither accurate nor complete. Regardless of whether there is an error in the process, the conversion error rate and associated confidence can be tested. However, if an error is detected at a given confidence level, the number of samples measured must be increased compared to the number of samples without errors.
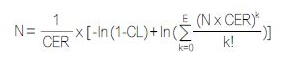
The above formula gives a natural logarithmic mathematical relational expression between confidence, bit error rate and number of samples. Where: N is the number of samples measured; CER is the conversion error rate; CL is the confidence; E is the number of errors detected.
When no error is detected, the formula is simplified, the item on the right is equal to zero, and the result depends only on the item on the left. When CL is 95% and no error is detected, the number of samples required is only about the inverse of the expected CER multiplied by 3. The 100% confidence is measured, that is, CL = 1.0 for any CER value, and it is mathematically necessary to obtain an infinite number of samples (N) of -ln(0) infinity.
Fiber Optic Connector,Fiber Connector,Fiber Termination,Fiber Adapter
Huizhou Fibercan Industrial Co.Ltd , https://www.fibercannetworks.com