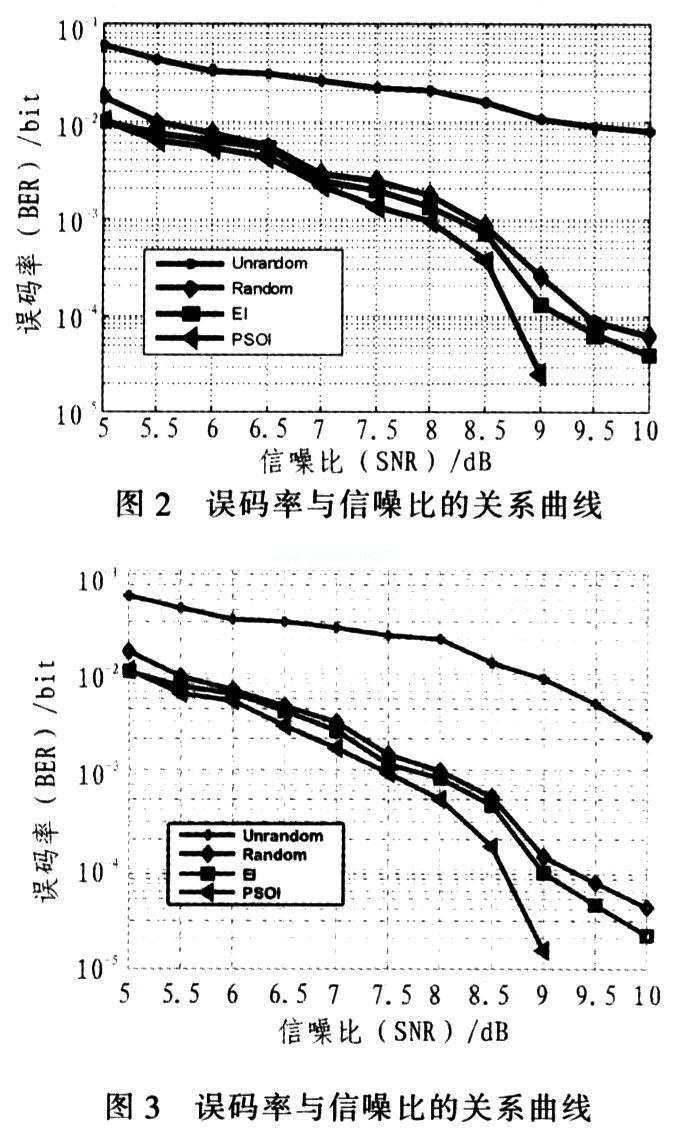
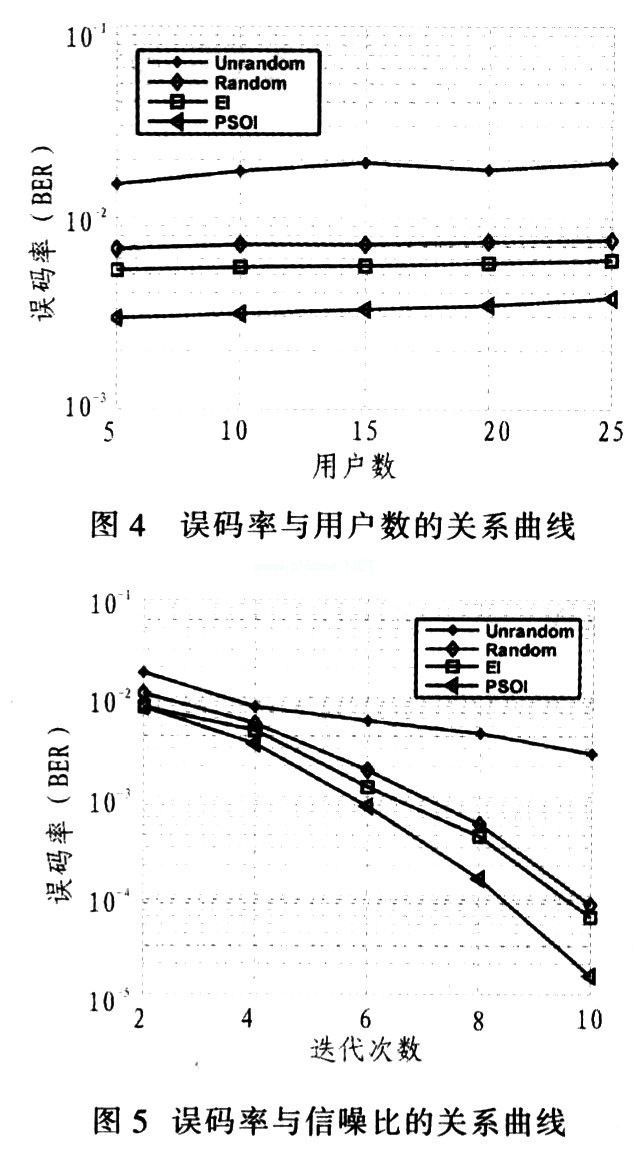
Particle Swarm Interleaving Algorithm in IDMA Communication System Introduction Advanced access technology code division multiple access (CDMA) can effectively use bandwidth, increase system capacity, and is widely used. IDMA interleaved multiple access is a special CDMA communication method that uses chip-level interleaved sequences to distinguish users. The interleaving sequence disrupts the original coding order, making adjacent chips almost irrelevant, and its receiving end uses a chip-to-chip iterative multi-user detection and reception method, and the calculation complexity is small. As the key technology of IDMA, the generation of interleaved sequences must be random and independent, and the correlation coefficient between the interleaved sequences is small. However, in practice, when the length of the data frame is small and the number of users is large, the correlation coefficient of the sequence after random interleaving is close to 1 with a large probability, so that the receiving end cannot correctly detect the user data, which seriously affects the communication performance. The literature proposes to use the cross-correlation function matrix as the fitness function to use the evolutionary algorithm to obtain the optimal interleaved sequence, but the evolutionary algorithm is prone to fall into the local optimal solution and cannot obtain the globally optimal interleaved sequence. In this paper, the particle swarm optimization algorithm is introduced into the interleaving algorithm, and the optimal solution can be obtained in a small number of iterations. At the same time, the interleaving performance in the case of large users is simulated. The experimental results show that this algorithm has better performance. 2 Detection principle and method in IDMA communication system Fig. 1 is the structure diagram of sending and receiving part of IDMA communication system. The sending end of the system includes K users, and the symbol sequence sent by the k-th user is: dk = [dk (1), ..., dk (i), ..., dk (I)] (I is the symbol length of the transmitted sequence ), The sequence after repeated code spreading with code length S is: Gk = [Gk (1), ..., Gk (j), ..., Gk (J)], J is the code length after spreading, and then After the interleavers are shuffled and rearranged, the transmission sequence becomes: Xk = [xk (1), ..., xk (j), ... xk (J)]. The receiving end of the system adopts Turbo-type iterative decoding structure, which is mainly composed of basic signal detector ESE, deinterleaver and K user decoders DEC. In the system, a fully synchronized memoryless channel is considered, and the received signal r (j) is expressed as: 3 Interweaving algorithm based on particle swarm In the formula, c1 and c2 are two positive constants, called acceleration factors, and r1 and r2 are random numbers distributed between [0, 1]. The steps of the particle swarm-based interleaving algorithm are: (1) Initialize the population, randomly generate an initial population index value and an initial replacement sequence, and generate a data matrix X according to the index value; (2) According to equations (10) and (11) Calculate the fitness function and save the global optimal solution 4 Performance simulation and analysis To test the performance of the particle swarm interleaving algorithm (PSOI), the algorithm is combined with non-random interleaving iterative detection (Un-random), random interleaving iterative detection (Ran-dom) and evolutionary interleaving iterative algorithm (EI) Compared. The simulation conditions are: uncoded Gaussian channel, channel fading coefficient hk = k, k∈ (1,2, ..., K), data symbol length I = 10; spreading symbol length S = 4; then interleaved symbols Length J = I × S = 40; N = 10 × K; all users use the same spreading symbols, loop iterative decoding 10 times, Monte Carlo simulation 10,000 times, particle swarm parameter setting: ω = 1, c1 = c2 = 2. Figure 2 shows the relationship between the bit error rate and signal-to-noise ratio of Un-random, Random, EI, and PSOI when K = 5. It can be seen from the figure that Un-random has the worst cross-correlation performance. When the signal-to-noise ratio is greater than 8 dB, the bit error rate of PSOI is close to zero, far superior to several other algorithms. Figure 3 shows the relationship between the bit error rate and signal-to-noise ratio of Un-random, Random, EI, and PSOI at K = 25. It can be seen from the figure that when the data chip length is small, the interdependence of Random's interleaved sequence is large, which reduces its performance; EI is easy to fall into the local optimal solution due to its poor search ability, which reduces the interleaving performance and PSOI Better. Figure 4 shows the relationship between the bit error rate of Un-random, Random, EI, and PSOI and the number of users when SNR = 6 dB. It can be seen from the figure that the bit error rate of PSOI as the number of users increases is lower than several other algorithms. However, due to the low signal-to-noise ratio, the bit error rate of EI is closer to PSOI. Figure 5 shows the relationship between the bit error rate of Un-random, Random, EI and PSOI and the number of iterations when SNR = 9 dB and K = 25. The figure shows. As the number of iterations increases, the bit error rate of the four methods will decrease, but the performance of PSOI is significantly better than several other algorithms. 5 Conclusion In this paper, the particle swarm optimization algorithm is used in interleaving, and the cross-correlation matrix is ​​used as the fitness function to propose a particle swarm optimization algorithm. Simulation shows that the performance of this algorithm is much better than non-random interleaving, random interleaving and evolution-based interleaving at high signal-to-noise ratio.
APM model SPS300VAC9000W 3 Phase Ac Power Source system is able to provide not only stable DC/AC output power,but also 3-phase / 1-phase output.The 3 Phase Ac Power Supply is with high speed DSP+CPLD control, high frequency PWM technology, active PFC design. Reliable ac sources for applications such as electric, lighting, aviation sectors, enterprise`s production test etc.
Some features as below:
9000W Three Phase Ac Source System 9000W Three Phase Ac Source System,System For Three Phase,Three Phase Power,Three Phase Power Supply APM Technologies (Dongguan) Co., Ltd , https://www.apmpowersupply.com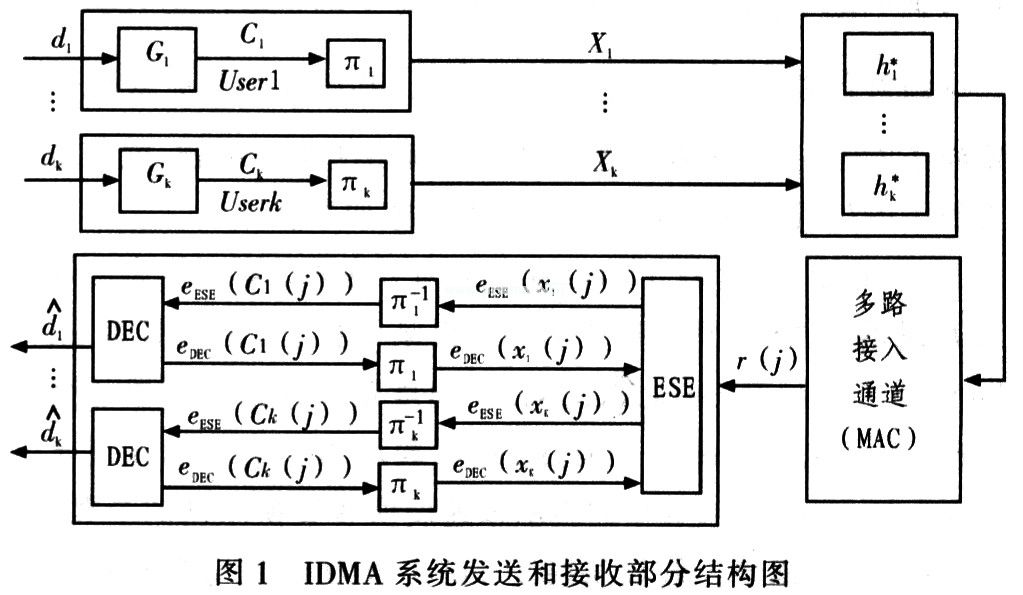
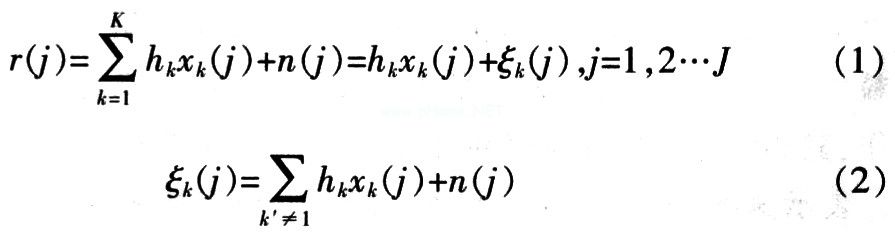
Where n (j) is Gaussian white noise sampling, hk is the channel fading coefficient of the kth user, ζk (k) is the distortion of the jth chip of the second user, and according to the central limit theorem, ζk (j) Meet the approximate Gaussian distribution, which can be expressed by the mean and variance functions.
The detection algorithm of the basic signal detector module ESE is summarized as follows: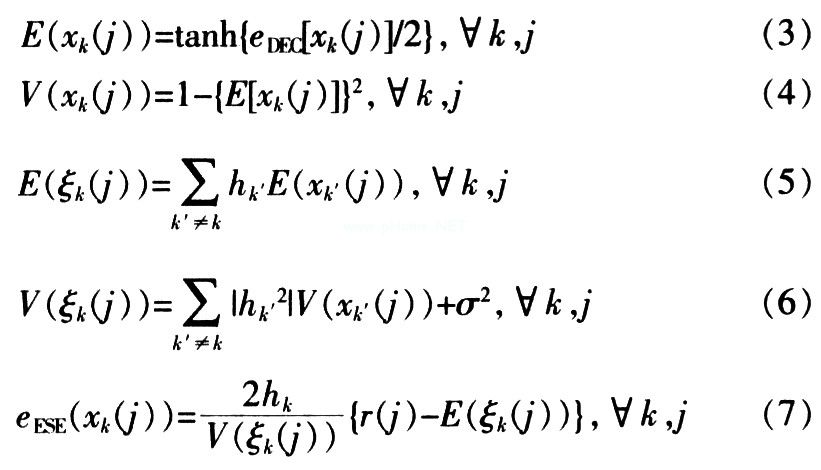 
In the formula, E (.) Represents the mean and V (.) Represents the variance.
The a priori information fed back by the decoder DEC is interleaved to obtain eDEC [xk (j)], the mean and variance of the received signal in the ESE are updated, and the external information eESE (xk (j)) input to the decoder DEC is generated, The external information is de-interleaved as a priori information at the input end of the decoder DEC. After the cyclic iteration until the specified number of times, the decoders of K users respectively generate hard decision values ​​dk of the corresponding information sequences.
3.1 Relevant definition and operation of particle swarm optimization particle swarm optimization algorithm is an iteration-based optimization method, has the advantages of easy implementation, less parameters to be adjusted, etc., and can obtain the global most in the case of fewer iterations Excellent solution. Let the number of particles in the particle swarm be M. In a D-dimensional search space, the position information of particle i (1≤i≤M) at the kth iteration is 
The speed information is expressed as an arbitrary number of search spaces, ie 
The best position the particle has experienced so far is 
The best position that all particles in the group have experienced so far is 
Where b is the index of the particle with the best position. In order for the particle swarm algorithm to correctly solve the interleaving problem, the meaning and related operations of defining the particle position and velocity are as follows:
(1) Particle definition The position of particles is defined as a sequence. For a population with a search space of D dimensions, the sequence length is D. Assuming that the position of a particle j is xj, D = 5, it can be expressed as xj = (1,2,3,4,5); the velocity is defined as the transformation set of the particle position, that is, an ordered list of a set of replacement sequences , Expressed as: v = {(ik, jk), ik, jk∈D}, k∈ {1,2, ..., | v |, where | v | represents the number of permutation sequences included in the velocity.
(2) Substitution operation Assuming that the position of a particle i is xi, define the substitution sequence (mi, ni). The substitution operation is used to exchange the position of the mi and ni values ​​in xi, then x'i = xi + (mi, ni) , Where x'i is the new position obtained after the replacement operation.
(3) The addition operation includes the addition operation of particle speed and velocity and the addition operation of particle velocity and position. Let vi, vj, and vk denote the velocity of the i-th, j-th, and k-th particles, respectively, and xk be the position of the k-th particle. vi + vj represents the operation of adding two velocities, and the result is that the two replacement sequences are combined to produce a new replacement sequence string; vk + xk represents the addition operation of velocity and position, that is, a set of replacement sequences are sequentially applied to a particle position. The result is a new location.
(4) Subtraction operation mainly refers to the subtraction operation of particle position and position. The result of the subtraction of this operation is a set of permutation sequences, namely speed. Let xk be the k-th particle position and xi the i-th particle position, then xi-xk is a substitution sequence. For example: xi = (1,2,3,4,5), xk = (2,3,1,4,5), because xi (1) = 1, xk (3) = 1, the first exchange sequence Is (1, 3), xj = xk (1, 3) = (1, 3, 2, 4, 5); and xi (2) = 2, xi (3) = 2, the second exchange sequence is ( 2, 3), xi = xj + (2, 3), so after the above operation we get: xi = xk + {(1, 3), (2, 3)}, so xi-xk = {(1, 3), ( 2, 3)}.
(5) The multiplication operation refers to the multiplication operation of the real number and the particle speed. For any real number c at (0,1), suppose that there are i permutation sequences for velocity v, then the multiplication operation intercepts the velocity permutation sequence, so that the number of new velocity permutation sequences is | cxi | (cxi rounded).
According to the above definition, the update formula of particle swarm can be described as: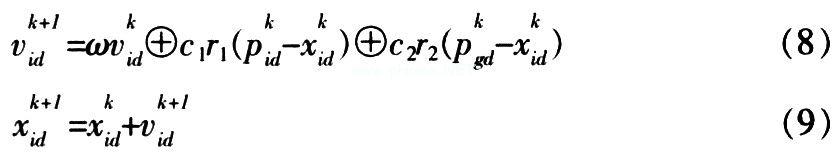 
3.2 Particle Swarm Interleaving Algorithm For sequences with a chip length of J, there are J! Kinds of interleaving methods. When J is small and the number of users is large, the number of interrelationships between randomly generated interleaved sequences is close to 1. When interleaving distinguishes users, the performance of communication between two users is seriously affected. The particle swarm algorithm can search for the global optimal solution, and can select the interleaved sequence with the weakest cross correlation to distinguish users, thereby improving communication performance.
In data transmission, the chip length J = IxS, where I is the symbol length of the transmission sequence. S is the length of the spreading code. Particle swarm interleaving selects K sequences with weak cross-correlation from J! Interleaved sequences to distinguish users, but J! Solutions have a large amount of calculation in actual operation, so N is selected as the initial solution. In the particle swarm interleaving algorithm, the cross-correlation matrix is ​​selected as the fitness function. X is a data matrix of N × J, which is N possible solutions, and each solution is an interleaved sequence of length J, whose elements are X (n, J) ∈ {-1,1} (n = 1, ..., N, j = 1, ..., J); INDEX represents a matrix of N × J, the value of which is the index value of the interleaved sequence corresponding to the data matrix X; R is the matrix of the correlation coefficients of X, which is N × N dimension, The element R (i, j) of R is calculated by the following formula: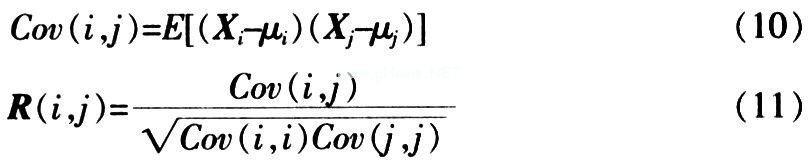 
In the formula, Xi is the i-th row vector of matrix X, μi = E (Xi), E represents the mathematical expectation. 
And local optimal solution 
; (3) Calculate the particle velocity according to equation (8). First calculate the local optimal solution 
Get the permutation sequence, and then calculate the global optimal solution 
Get another permutation sequence, multiply it by the coefficient and intercept 
Merged 
(4) Update the current particle index value according to equation (9), and update the data matrix X value according to the index value; (5) Recalculate the fitness function and update 
(6) If the maximum number of iterations is reached, the algorithm terminates; otherwise, go to step 2. 
