1 Introduction Topology is a branch of mathematics that studies the properties of geometric shapes or spaces that remain unchanged after successively changing shapes, such as stretching, wrinkling, and bending, but without tearing or bonding, important topological properties. Includes connectivity and compactness. By analyzing concepts such as space, dimensions, and transformation, topology development has become a research field of geometry and set theory. The Königsberg Seven Bridge Problem and the Polyhedral Formula proposed by Leonhard Euler can be said to be the first theorem in this field, representing the birth of topology. Although the concept of topological space was proposed in the early 20th century, the term topology was proposed as early as the 19th century Johann Benedict Listing. By the middle of the 20th century, topology had become an important branch of mathematics. The concept of topology has also been extended to other disciplines, such as the study of the effects of enzymes on DNA in biology through knot theory; the use of geometric topology in computer science for topological data analysis; in physics, Topological concepts are used in the fields of condensed matter physics, quantum field theory, and physical cosmology. The application of topology in condensed matter physics can be traced back to the 20th century. In 1960, two scientists, Thouless and Kosterlitz, theoretically derived theoretical models of vortex motion in a two-dimensional superfluid/superconducting system in real space. They found that there is a phase in the system with temperature changes. Disorder to the special phase transition of the "quasi-length program" (Kosterlitz-Thouless phase transition), which is caused by the vortex free state to the bound state transition. Later, people found that in addition to real space, there is a rich and wonderful topology in the inverted space (momentum space). In 1980, Von Klitzing discovered the integer quantum Hall effect in low temperature and strong magnetic fields. In 1982, Thouless et al. proposed a topological classification of electronic state wave functions and found the TKNN invariant, the Chern number. With this integer, all two-dimensional insulator states can be classified. At that time, people realized the material state with non-zero number in the artificial system of quantum Hall effect system formed by two-dimensional electron gas under strong magnetic field, and the natural crystal material with non-zero number can only Looking for a system of time-reversed symmetry breaking (with spontaneous magnetism). In 2005, Kane/Mele and Bernevig/Zhangshouyi were based on graphene and semiconductor quantum wells under special stress fields, respectively, and almost simultaneously proposed a spin Hall effect system (or topological insulator) described by spin Chern number. This two-dimensional insulator with time inversion can be divided into two types of parity, mathematically called Z2 classification, in which odd classes have Dirac-type boundary states symmetrically protected by time inversion, while even classes do not. A protected boundary state. The discovery of quantum Hall effect, quantum spin Hall effect and topological insulators has completely changed people's cognition of condensed matter physics and stimulated the study of topological phenomena in other fields. In recent decades, the concept of photon/phonon crystals and light/acoustic superstructure materials has been proposed to achieve more efficient manipulation of conventional waves, such as light/sound zero-density materials, super-transmission, stealth cloaks, and focusing. And other functions. At the same time, the discovery of superstructure materials also laid the foundation for the study of optical/acoustic topography. First of all, in the field of optics, topological phase transitions are realized in two-dimensional space by means of a gyromagnetic photonic crystal, a bi-anisotropic superstructure material, and a coupled optical waveguide. Due to the similarity between acoustic wave equation and optical wave equation, the study of acoustic topological phase has become a research hotspot in recent years. Acoustic topological protection of boundary state transmission can suppress backscattering well and is robust to defects, making it It has great application prospects in acoustic communication, noise control, and acoustic and electrical integration. This paper will focus on the acoustic topological state and its related problems, and introduce the related work of quantum-like Hall effect, Floquet topological insulator, quantum-like spin Hall effect and valley-like Hall effect in two-dimensional acoustic systems in recent years. 2 Acoustic quantum Hall effect The realization of the quantum Hall-like effect needs to break the T symmetry (time reversal symmetry), which can be realized by external magnetic field, etc., but for the sound wave lacking the magnetic field and only the longitudinal wave mode, how to break T or how to construct, etc. The effective magnetic field is an urgent problem to be solved. In 2014, Romain Fleury et al. proposed a method to break the time inversion symmetry by using the annular velocity field and construct an acoustic isolator. This finding provides the possibility to realize the acoustic quantum Hall effect. In 2015, Zhaoju Yang et al. (the other two research groups in the same year) used the background velocity field to be equivalent to the magnetic field in a two-dimensional acoustic system and constructed a unidirectional boundary transmission state protected by topology. The research team starts from the triangular lattice that can form the Dirac degenerate point, on the periphery of each unit (r1 Where r is measured from the center of the unit. Assuming that viscous and heat flow can be ignored, the acoustic master equation satisfies: Where Ï is the density of the fluid, c is the speed of sound, and v0 is the background flow rate. Under the coordinate transformation Ψ = âˆšÏ Ï†, the formula (1) can be written as follows: Where the effective vector potential Aeff = - ωv0(x, y) / c2 , the scalar potential V (x, y) = - 1/4 | ∇ ln Ï | 2 - 1/2 ∇ 2 ln Ï + ω2 / c2 . The effective vector potential generated by the annular velocity field produces an equivalent magnetic field Beff = ∇ × Aeff . As shown in Fig. 1(b), due to the time-reversal symmetry breaking caused by the equivalent magnetic field after the flow rate is added, the Dirac cone originally generated at the boundary of the first Brillouin zone in the energy band diagram It is opened to create a band gap. By calculating the Berry connection and the number of counts: It can be obtained that the number of the two energy bands shown in Fig. 1(b) is +1 and -1, according to the "body-boundary correspondence" principle, for a finite phonon crystal based on such a triangular lattice, these two There will be a one-way acoustic topological boundary state in the band gap between the strips. As shown in Fig. 1(c), when the flow velocity Ω = 2Ï€ × 400 rad / s, a one-dimensional transmission in the opposite direction of the group velocity is formed in the band gap of the one-dimensional phononic crystal (20 cells in the y direction, infinite in the x direction). The boundary states correspond to the upper and lower boundaries, respectively. As shown in Fig. 1(d), a 34×14 finite-large phononic crystal is further constructed, and an acoustic wave is incident at the upper boundary at a frequency of ω0 = 0.577 × 2Ï€c/a, and the acoustic wave will be transmitted in one direction along the boundary. Since there is no back-transport boundary state, the defect will not cause backscattering, so the introduction of defects such as cavities and curved paths on the boundary (Fig. 1(d)) will not affect the one-way transmission of sound waves, which can guarantee High transmission efficiency. Figure 1 (a) Two-dimensional triangular lattice under the background velocity field; (b) No velocity field (red curve, Ω = 2Ï€ × 0 rad/s) and velocity field (blue curve, Ω = 2Ï€ × 400 rad /s) Energy band structure of the lower phononic crystal; (c) One-dimensional phononic crystal band structure, red curve indicates topological boundary state, blue curve indicates body state; (d) boundary is free of defects, cavity and Sound pressure distribution under three conditions of bending However, this topology requires simultaneous coordination of the velocity fields around all of the cells and guarantees the same flow rate, and the losses and noises inherent in it make it difficult to implement and manipulate in experimental and practical applications. 3 Acoustic Floquet Topology Insulators Adding the background velocity field to break the time to invert the symmetry and constructing the quantum Hall effect method brings inherent loss and noise, which limits its application. In order to solve this problem, in 2016, Romain Fleury et al proposed A method of time and space modulation in a hexagonal lattice and an acoustic Floquet topology insulator was constructed. This theoretical model is based on slow modulation of lattice rotation, with the advantage that no uniform phase is required between the lattices. As shown in Fig. 2(a), there is a trimer at each lattice point of the hexagonal lattice, which can be equivalent to 3 acoustic volumes C0 = β0V0, so a trimer composed of 3 cavities can wait The effect is the LC resonant circuit. In order to break the time-inversion symmetry structure topology non-mean characteristics, a time-dependent local potential ΔCm(t) = δC cos(ωmt - φm) can be used to modulate the acoustic capacitance of each cavity with a modulation intensity of δC/C0. The frequency is fm = ωm/2Ï€, and the phase φm depends on each sub-cavity m, so this modulation applies an equivalent spin to each trimer, thus breaking the time-reversal symmetry (Fig. 2(b) ). As shown in Fig. 2(c), the weak air conditioning system will have an effect on the energy band structure of the phononic crystal. In the absence of modulation, four transmission bands will be generated around 22 kHz, corresponding to the energy band with the group velocity approaching zero and the fast Dirac band, due to the time-reversal symmetry of the crystal and the combined space-time inversion Symmetry, these four bands will be degenerate at the Γ and Κ points. Further research found that when the modulation δC/C0 = 6% and fm = 2 kHz are introduced, the energy band will translate along the frequency axis in the period of ωm, and the degenerate state at the Γ and Κ points is opened, the size of the opening and Modulation intensity is related. Using the equivalent Hamiltonian of the time-dependent compact-bound state model, the Hamiltonian of this hexagonal lattice can be rewritten as Where |m> = |m1,m2,m3 > corresponds to the three acoustic cavities that make up the hexagonal lattice grid. Introducing a stroboscopic evolution operator at every cycle t=nT of the system Time-dependent equivalent Hamiltonian can be written as , and then use the equivalent eigenstate of the Hamiltonian |pn> and Bailey contact A=-i< pn| ∂k| pn> to get the number Cn = 1/2Ï€ ∫BZ(∂kx Ay - ∂ky Ax ) D2k , the four energy bands are Cn = {1,0,0, - 1}, respectively, and it can be found that the system changes from a mediocre state to a non-planar state when modulation is applied. Further research has found that such a phononic crystal made by air conditioning has a topologically protected boundary state transmission phenomenon. Although the theoretical model of acoustic Floquet topological insulator has been proposed, it is difficult to experimentally implement periodic time-dependent modulation. Therefore, in practical applications, the Floquet topological state without time is needed. In 2016, Yugui Peng et al. proposed a method for constructing acoustic Floquet topological insulators using a coupling model between superconducting material waveguides and experimental verification. As shown in Fig. 2(d), a unit of the two-dimensional lattice consists of a centrally located lattice ring and four surrounding coupling rings, each of which is periodically arranged by a subwavelength-sized air-metal layer. a metamaterial waveguide ring (Fig. 2(e)), the equivalent refractive index of this structure is Where t, w is the thickness and width of the metal plate, p is the period of the structure, and ω = 2Ï€f represents the angular frequency of the acoustic wave. The transmission direction of sound waves in the lattice ring is defined as èµ spin, that is, clockwise is èµ spin upward, counterclockwise is èµ spin down, artificially designed crystal structure can construct topological boundary supporting èµ spin-orbit coupling Transmission state. By calculating the energy band structure of a semi-infinite crystal composed of such cells, it is found that a unidirectional topological boundary state is generated in the band gap, as shown in Fig. 2(f)-(i), further through finite element simulation and Experiments verify the boundary state of the spin-orbit coupling topology. It should be noted that in this model, the two acoustic èµ spin states are completely decoupled, so the defect immunity of this topological state is limited to In the case of non-reversal rotation, high machining accuracy is required. The superstructure material acoustic waveguide can also be replaced by some water acoustic ring coupling model or air acoustic ring coupling model to realize the Floquet topological insulator of the two-dimensional acoustic system. Figure 2 (a) hexagonal lattice formed by acoustic trimer, gray material is silicone rubber; (b) primary base cell of hexagonal lattice, giving each cavity a sound volume C = C0 + ΔC( t) Applying a cyclic form of time periodic modulation, the frequency is ωm, the modulation amplitude is δC, which can produce a chirality in the crystal; (c) the band structure after applying the time modulation (blue curve) (orange curve) Contrast; (d) a structural diagram of a two-dimensional coupled metamaterial ring lattice; (e) a detailed view of the air-metal structure; (f, g) simulation and experiment of the sound field amplitude of the spin-up boundary state Results; (h, i) simulation and experimental results of the amplitude of the sound field transmitted by the spin-down boundary state, the distance between two adjacent lattice rings is 2D 4 Acoustic quantum spin Hall effect Electron spin-orbit coupling brings many fascinating phenomena and important applications, including topological insulators and spintronics. We all know that electrons are fermions, and photons/phonons are bosons. The fundamental difference between sound waves and electrons leads to the loss of spin degrees of freedom in the acoustic system. Although we can construct acoustic topologies by applying velocity fields and coupled acoustic waveguides to construct acoustic topologies, the harsh external conditions, fine industrial processing requirements, and large size limitations of these methods are limited. The actual application. In 2017, Professor Liu Xiaojun of Nanjing University proposed theoretically the construction of acoustic èµ spin dipole and quadrupole modes in supermaterial phononic crystals with no flow velocity background, and realized the universal theory of tunable acoustic wave topology transmission. method. First, as shown in Fig. 3(a), the primary cell of the honeycomb lattice phononic crystal is rotated by 30° and enlarged, so that the honeycomb lattice becomes a triangular crystal composed of supercells composed of 6 cells. The lattice is then formed into a double Dirac cone by the band folding theory (Fig. 3(b)). In this system, the èµ time inversion symmetry comes from the symmetry of the phononic crystal, and the èµ time inversion operator satisfies: Among them, DE1(C6) and DE1(C62) represent the 60° and 120° rotation operations under C6 rotational symmetry, σy is the Pauli matrix, and K is the complex conjugate operator, so in this phononic crystal The time-reversed protection property of T2 = -1 is satisfied. Then, by keeping all the cells unchanged, it is possible to break the double Dirac cone to form a band gap by merely shrinking or expanding the pitch (R) of each cell in the supercell. It is found that the sound pressure field distribution near the band gap exhibits a symmetrical form similar to the electronic p/d orbit, and the average sound intensity rotates clockwise or counterclockwise, which is different from the traditional acoustic multipole mode. Effective acoustic èµ spin dipole and quadrupole. According to the classical acoustic theory, in the traditional acoustic multipole mode, the acoustic energy radiates outward in a fixed azimuth and cannot form a rotating sound field. The èµ spin multipole formed in the phononic crystal is a novel phenomenon of the two-dimensional acoustic system. Further exploration offers possibilities. The study further found that when the supercellular intracellular unit is contracted, the frequency of the èµ spin dipole mode (sound pressure p symmetric distribution) is below the èµ spin quadrupole mode (sound pressure d symmetric distribution), consistent with the traditional acoustic theory. When the super-cell intracellular cell spacing is expanded, the èµ spin dipole mode frequency jumps above the spin quadrupole mode. At the same time, in this acoustic system, the Z2 topological invariant is calculated by the Bailey curvature, ie the number can be reduced to: Where B is from the second-order perturbation term and is negative, and εp / εd corresponds to the eigenstate when the sound pressure p/d is symmetrically distributed. According to the theoretical analysis, when the supercell unit spacing is reduced, M>0, so the number C±=0, the band gap is trivial; when the supercell unit spacing is expanded, M<0, so the number C± =±1, the band gap is nontrivial. In general, as shown in Fig. 3(c, d), the inter-cell spacing is changed from small to large, and the energy band is reversed. The topological state undergoes a change from a mediocre state to a non-definite state. Figure 3 (a) A triangular lattice consisting of a supercell (R/a = 1/3) containing 6 units; (b) an energy band structure obtained by band folding theory; (c) by shrinking and expanding The super-cell intracellular unit spacing breaks the double Dirac cone to form a band gap; (d) the p/d orbital reversal, that is, the energy band reversal; (e) the one-dimensional strip phononic crystal structure and its energy band structure; f) Topological boundary state sound pressure and sound intensity field distribution In this topology, the pattern hybridization between the two degenerate Bloch states forms a spin-up and a spin-down. As shown in Fig. 3(e, f), an acoustic topological boundary state in which the sonar spin is coupled with the transmission orbit can be formed on the boundary between the mediocre and non-planar phononic crystals, successfully in the two-dimensional acoustic system. A quantum-like spin Hall effect is constructed, and the coupling of the èµ spin state and the acoustic transmission path forms a classical "4=2+2" orbit similar to that in the electronic system: the spin-down state propagates to the right at the upper boundary, at the lower boundary. Propagating to the left; the spin-up state propagates to the left at the upper boundary and to the right at the lower boundary. It is found that in the topological band gap, the boundary state transmission between the two spin states of the same frequency or different frequencies does not cause interference, and the adjustable and arbitrary shape can be realized by adjusting the spacing of the supercell intracellular elements. The topological boundary, which is very beneficial for practical applications. At the same time, this topologically protected boundary state possesses backscatter suppression and good robustness. Cavities, disordered alignment and bending defects on topological boundaries not only cause backscattering, but also do not change the boundary sound. The spin state of the transmission. This universal method of generating acoustic èµ spin multipole modes can be further extended to various basic acoustic systems such as “gas-liquidâ€, “solid-liquidâ€, and “solid-gasâ€. The Lu Minghui and Chen Yanfeng research groups of Nanjing University also found a double Dirac cone formed in the center of the Brillouin zone due to accidental degeneracy in the C6v symmetry phononic crystal, which is different from the energy band folding theory mentioned above. The energy band inversion of p/d symmetry can be realized by adjusting the duty cycle. In order to study the chiral propagation characteristics of the acoustic topological boundary state, an "x" type splitter model is designed. The sound waves that make the spin-up and the spin-down are completely different inlet and outlet channels, thus spatially separating the two types of phonons that spin up and down. At the same time, they verified the robust one-way transmission of this kind of quantum spin Hall effect acoustic topological insulator. 5 soot transport It is well known that electrons have two intrinsic degrees of freedom, namely charge and spin. In addition to these two degrees of freedom, solid materials also have a valley degree of freedom, and valleys are extreme points in the band structure, which are not only widely found in conventional semiconductor materials, but also in the current hot two. In the dimensional crystal, such as graphene, molybdenum disulfide, and the like. The definition of valley degrees of freedom is similar to the spin freedom of electrons, so the valley degree of freedom is also called èµ spin, and the information processing using valley degrees of freedom has the information not easy to lose, the processing speed is fast, the energy consumption is small, and the integration is high. , the transmission distance is far and so on. In 2016, the research team of Wuhan University Liu Zhengyu introduced the concept of the valley state of the electronic system into a two-dimensional phononic crystal, and found the topological boundary state acoustic transmission on the boundary between two phononic crystals with different valley Hall phases. As shown in Fig. 4(a), the rotatable equilateral triangle scatterers are arranged in a triangular lattice, the background medium is air, the lattice constant is a, and α is a rotation angle, where p and q represent two of the fluid bases. The lattice center of the price. It can be seen that when the rotation angle is α = 0°, the phononic crystal has C3 symmetry, and the band structure will form a Dirac cone at the K and K' points of the first Brillouin zone. When the rotation angle is deflected (-60° < α < 60°), the mirror symmetry mismatch of the equilateral triangle scatterer and the lattice is opened, and the Dirac cone in the band structure opens to form a band gap, forming a band on both sides of the band gap. The extreme point, which is the valley state, is shown in Figure 4(b). Since the K and K' points can be converted by the time inversion operation, the sound pressure field and the sound intensity field corresponding to the K point valley state can be mainly studied. The study found that, similar to the valley state of the electronic system, the acoustic valley state is also chiral, and an acoustic vortex field is formed between the scatterers. As shown in Fig. 4(c), if the direction of the vortex is reversed and clockwise is rotated by the +, -, the p, q mark produces the position of the vortex, then when α < 0, the upper valley state is q+. The lower valley state is p-; when α>0, the upper valley state is p-, and the lower valley state is q+. Explain that during the process of rotating the scatterer, the energy band undergoes the process of opening-closing-opening, and the vortex characteristics of the valley are exchanged when the rotation angle α = 0°, similar to the electronic system, where the gluten spin Reversal means that a valley Hall phase transition has occurred. Figure 4 (a) A phononic crystal constructed from an equilateral triangle scatterer at a triangular lattice point; (b) a rotation angle of the scatterer α = 0° (black line) and α = -10° (color line) The lower dispersion curve; (c) the change of the valley frequency with the scatterer angle, the valley field distribution with α = ±10°; (d) the scatterer with the angle α = 10° and 50° The energy band structure diagram of the phononic crystal. The following figure shows the energy band structure of the phononic crystal composed of scatterers with angles α = -10° and 10°, indicating that the topological boundary is supported on the boundary between different valley Hall phases. State transmission; (e) parity-excited excitation and (f) momentum selective excitation of boundary state The sonar Hall phase transition in this system can be described by an α-dependent continuous Hamiltonian, which can be derived from the k·P perturbation theory, whose base vector space is degenerated by degenerate valence state 6 Conclusion In recent years, the rapid development of topological effects in two-dimensional acoustic systems has made topological acoustics a research hotspot, and theoretical models of topological acoustics in three-dimensional space have also been proposed. The construction of tunable acoustic topological insulators with wider band boundary states requires further study. From the application point of view, scientists will further study acoustic devices based on different topological properties, such as acoustic stealth, unidirectional lossless transmission of acoustic signals, and noise. Control, these are expected to have a huge impact on the military, medicine and industry. Automatic soap dispenser foam Intelligent Dispenser Soap Dispenser Holder Ningbo ATAP Electric Appliance Co.,Ltd , https://www.atap-airfryer.com
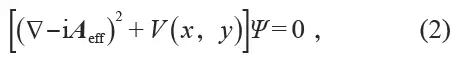
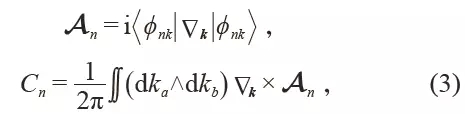
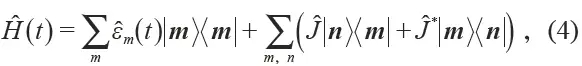
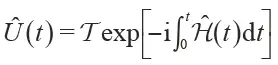
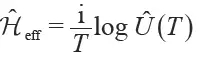
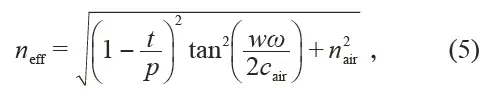
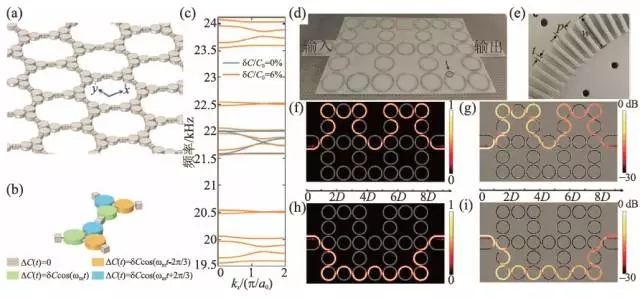
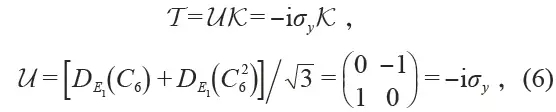
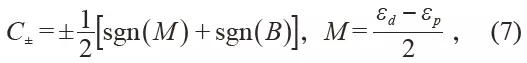
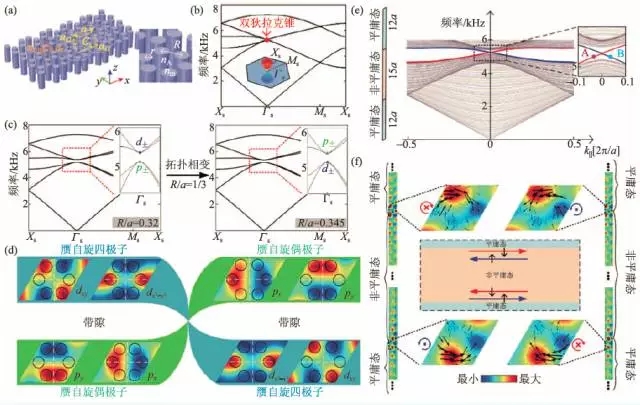
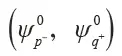Zhang Cheng, the Hamiltonian form is δH= vDδkx σx + vDδky σy +mvD2σz . Where vD is the Dirac velocity when the Dirac cone is formed by α = 0°, δk is the momentum deviating from the K point in the momentum space, σi is the Pauli matrix, and the equivalent mass is defined as m=(ωq+ - ωp- )/2vD2 , ωq+ /ωp- corresponds to the characteristic frequency of the valley èµ spin q+/p-, so different valley Hall phases can be represented by the sign of the effective mass. Similar to the graphene system, the non-mean Pele curvature Ω(δk) = 1/2 mvD(δk2 +m2vD2)-3/2 can be obtained by the Hamiltonian δH, which can be obtained by integrating it in the Brillouin zone. Zero topological charge CK = sgn(m)/2. For a boundary state between different valley Hall insulators, the change in topological charge on both sides is quantized ( |ΔCK| = 1), which means that a chiral boundary transport state is produced. For example, from the symmetry of the crystal, the energy band structure of phononic crystals with α = -10° , α = 10° and α = 50° is the same, but at α = -10° and α = 10° On the boundary between different valley Hall-phase phononic crystals, due to the reversal of the equivalent mass, a pair of valley chiral boundary transport states can be generated in the band gap, as shown in Fig. 4(d). However, α = 10° and α = 50°. The two phononic crystals have the same valley Hall phase because no equivalent mass reversal occurs, and no topological boundary states are generated in the band gap. It is found that the topological valley Hall boundary state is essentially derived from the physical properties of a single valley. This implies two meanings: the boundary state dispersion curve is derived from an independent valley projection; the wave function is composed of a linear superposition of degenerate base states of the same valley. . Decoupling between valleys leads to many interesting boundary transport phenomena, such as the parity/momentum selective excitation of the boundary state and the anti-reflective effect of the boundary state.